User:Netshine2/sandbox

Constricting the pass band ripple

Standard low pass Chebyshev filter design creates an equi-ripple pass band beginning from 0 rad/sec. However, some design requirements do not need an equi-ripple pass band at the low frequencies. A standard full-equi-ripple Chebyshev filter for this application would result in an over designed filter. Constricting the equi-ripple to a defined percentage of the pass band creates a more efficient design, reducing the size of the filter and potentially eliminating one or two components, which is useful in maximizing board space efficiency and minimizing production costs for mass produced items.

Constricted pass band ripple can be achieved by designing an asymmetric Chebyshev band pass filter using the techniques described in this article with a 0 order asymmetric high pass side and an $\omega 2$ set to the constricted ripple frequency. This results in a less than unity S12 at $\omega =0$, which is typical of even order standard Chebyshev design, so for standard even order Chebyshev designs, the process is complete at this step. If the less than unity S12 at $\omega =0$ is objectionable for other designs, it will be necessary to insert a single reflection zero at $\omega =0$ for odd order designs, and two reflection zeros at $\omega =0$ for even order modified designs. If reflection zeros are added, a noticeable error will be introduced in the pass band that is likely to be objectionable. This error may be removed quickly and accurately by positioning the finite reflection zeros with the use of Newton's method for systems of equations.

Application of Newton's method

Positioning the reflection zeros with Newton's method requires to pieces of information:

1. The location of each pass band ripple minima that exists at frequencies higher than the constricted ripple frequency.
2. The partial derivative of each reflection zero with respect to each pass band minima of the magnitude normalized $K(s)$, that is $|K(s)|=1$ at $\omega =1$.

Since the characteristic equations, $K(s)$ has all reflection zeros located on the $j\omega$ axis, and all the transmission zeros either on the $j\omega$ axis or symmetrical bout the $j\omega$ axis (required for passive element implementation), the locations of the pass band ripple minima may be obtains by factoring the numerator of the derivative of $K(s)$, $(dK(s)/ds)_{num}$, with the use of a root finding algorithm. The roots of this polynomial will be the pass band minima frequencies.

To obtain the partial derivatives of the reflections zeros with respect to $|K(s)|=1$, a continuous expression for $K(s)$ needs to be obtains that forces $|K(s)|=1$ at all times. This may be achieved by expressing $K(s)$ as a function of its conjugate root pairs, as shown below.

${\begin{aligned}K(s)&={\begin{cases}K_{finite}(s)&{\text{if }}n{\text{ is even}}\\sK_{finite}(s)&{\text{if }}n{\text{ is odd}}\\\end{cases}}\\&\\K{finite}(s)&={\frac {\prod _{i=1}^{N_{Rp}}(R_{i}^{2}+s^{2})}{\prod _{i=1}^{N_{Tp}}(T_{i}^{2}+s^{2})}}{\frac {\prod _{i=1}^{N_{Tp}}(T_{i}^{2}-1)}{\prod _{i=1}^{N_{Rp}}(R_{i}^{2}-1)}}\\\end{aligned}}$

Where $K{finite}(s)$ includes finite reflection and transmission zeros, only, $N_{Rp}$ and $N_{Tp}$ refer to the number of reflection and transmission zero conjugate pairs, and $R_{i}$ and $T_{i}$ are the reflection and transmission zero conjugate pairs. Note that if quadruplet transmission zeros are employed, the expression must be modified to accommodate quadruplet terms. It is easily seen by inspection that $|K(s)|=1$ whenever $\omega =1$in the above expression.

///////////////////////////////////////////////////////////////////////////////////////////////

Hourglass filter

An Hourglass filter is a special case of filter where the reflection zeros, are the reciprocal of the transmission zeros about a 3.01 dB normalized cut-off attenuation frequency of 1 rad/sec, resulting all poles of the filter residing on the unit circle. The Elliptic Hourglass implementation has an advantage over an Inverse Chebyshev filter in that the pass band is flatter, and has an advantage over traditional Elliptic filters in that the group delay has a less sharp peak at the cut-off frequency.

7 pole Hourglass reciprocal S11 and S12 frequency response

Syntheses process

The most straightforward way to synthesize an Hourglass filter is to design an Elliptic filter with a specified design stop band attenuation, As, and a calculated pass band attenuation that meets the lossless two-port network requirement that scattering parameters $|S_{11}|^{2}+|S_{12}|^{2}=1$. Together with the well known magnitude dB to arithmetic translation, $(S_{ij})_{dB}=20log_{10}(|S_{ij}|_{arith})$, algebraic manipulation yields the following pass band attenuation calculated requirement.

$A_{p}=-10\log _{10}{(1.-10^{(-A_{s}/10)})}$

The A_p, defined above will produce reciprocal reflection and transmission zeros about a yet unknown 3.01 dB cut-off frequency. to Design an Elliptic filter with a pass band frequency of 1 rad/sec the 3.01 dB attenuation frequency needs to be determined and that frequency needs to be used to inversely scale the Elliptic design polynomials. The result will be polynomials with an attenuation of 3.01 dB at a normalized frequency of 1 rad/sec. Newton's method or solving the equations directly with a root finding algorithm may be used to determine the 3.01 dB attenuation frequency.

Frequency scaling with Newton's method

If $G(s)$ is the Hourglass transfer function to find the 3.01 dB frequency, and $\omega _{c}$ is the 3 dB frequency to find, the steps below may be used to find $\omega _{c}$

1. If $G(s)G(-s)$ is not already available, multiply $G(s)$ by $G(-s)$ to obtain $G(s)G(-s)$.
2. negate all terms of $s^{n}$ when $(n+2)$ is divisible by $4$. That would be $s^{2}$, $s^{6}$, $s^{10}$, and so on. The modified function will be called $G_{2}(s)G_{2}(-s)$, and this modification will allow the use of real numbers instead of complex numbers when evaluating the polynomial and its derivative. the real $\omega _{a}$can now be used in place of the complex $j\omega _{a}$
3. Convert the desired attenuation in dB, $A_{dB}$, to a squared arithmetic gain value, $B_{arith}^{2}$, by using $B_{arith}^{2}=10^{A_{dB}/10}$. For example, 3.010 dB converts to 0.5, 1 dB converts to 0.79432823 and so on.
4. Calculate the modified $|G_{2}(s)G_{2}(-s)|$ in Newton's method using the real value, $\omega _{a}$. Always take the absolute value.
5. Calculate the derivative the modified $G_{2}(\omega _{a})G_{2}(-\omega _{a})$ with respect to the real value, $\omega _{a}$. DO NOT take the absolute value of the derivative.

When steps 1) through 4) are complete, the expression involving Newton's method may be written as:

$\omega _{a}=\omega _{a}-([G_{2}(\omega _{a})G_{2}(-\omega _{a})|-B^{2})/(d[G_{2}(\omega _{a})G_{2}(-\omega _{a})]/d\omega _{a})$

using a real value for $\omega _{a}$with no complex arithmetic needed. The movement of $\omega _{a}$ should be limited to prevent it from going negative early in the iterations for increased reliability. When convergence is complete, $\omega _{a}$ can used for the $\omega _{c}$ that can be used to scale the original $G(s)$ transfer function denominator. The attenuation of the modified $G(s)$ will then be virtually the exact desired value at 1 rad/sec. If performed properly, only a handful of iterations are needed to set the attenuation through a wide range of desired attenuation values for both small and very large order filters.

Frequency scaling with root finding

Since $|G(j\omega _{a})|$ does not contain any phase information, directly factoring the transfer function will not produce usable results. However, the transfer function may be modified by multiplying it with $G(-s)$ to eliminate all odd powers of $G(j\omega a)$, which in turn forces $G(j\omega a)$ to be real at all frequencies, and then finding the frequency that result on the square of the desired attention.

1. If $G(s)G(-s)$ is not already available, multiply $G(s)$ by $G(-s)$ to obtain $G(s)G(-s)$.
2. Convert the desired attenuation in dB, $A_{dB}$, to a squared arithmetic gain value, $B_{arith}^{2}$, by using $B_{arith}^{2}=10^{A_{dB}/10}$. For example, 3.010 dB converts to 0.5, 1 dB converts to 0.79432823 and so on.
3. Find $P(S)=G_{num}(S)G_{num}(-S)-B_{arith}^{2}G_{den}(S)G_{den}(-S)$
4. Find the roots of P(S) using a root finding algorithm.
5. Of the set of roots from above, select the positive imaginary root for off order filters, and positive real root for even order filters for $\omega _{c}$.

Scaling the transfer function

When $\omega _{c}$ has been determined, the Hourglass transfer function polynomial may be scaled as follows:

${\begin{aligned}G(s)_{\text{orig}}&={\frac {N_{nn}s^{nn}+\dots +N_{2}s^{2}+N_{1}s+N_{0}}{D_{nn}s^{nd}+\dots +D_{2}s^{2}+D_{1}s+D_{0}}}{\text{ (original unscaled transfer function polynomials)}}\\G(s)_{\text{ scaled}}&={\frac {N_{nn}(\omega _{c}s)^{nn}+\dots +N_{2}(\omega _{c}s)^{2}+N_{1}\omega _{c}s+N_{0}}{D_{nn}(\omega _{c}s)^{nd}+\dots +D_{2}(\omega _{c}s)^{2}+D_{1}\omega _{c}s+D_{0}}}{\text{ (}}3.01{\text{ dB at 1 rad/sec scaled transfer function polynomials)}}\\\omega _{c}&=|G(s)|{\text{ 3.01 dB attenuation frequency }}\\nn,nd&={\text{ order of numerator and denominator, respectively}}\\N,D&={\text{ coefficients of numerator and denominator, respectively}}\\\end{aligned}}$

Even order modifications

Even order Hourglass filters have the same limitations regarding equally terminated passive networks as other Elliptic filters. The same even order modifications that resolve the problem with Elliptic filters also resolve the problem with Hourglass filters.

/////////////////////////////////////////////////////////////////////////////////////////////

filter

Setting the cutoff attenuation

There is no standard set attenuation value for Bessel filters. However, −3.0103 dB is a common choice. Some applications may use a higher or lower attenuation such as −1 dB or −20 dB. This can be approximated by interpolating Bessel filter attenuation tables, or calculated with high accuracy with Newton's method or a root finding algorithm. See the draft Filter design process page for details on setting the attenuation cutoff frequency.

For example, a 20 dB cut-off frequency attenuation example using the 3 pole Bessel example below is set as follows.

${\begin{aligned}&H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}{\text{ (from the example below)}}\\&B_{arith}^{2}=10^{20/10}=0.01{\text{ (the arithmetic gain squared)}}\\&\\&{\text{find }}H(s)'{\text{ such that }}|H(s)'|=-20dB{\text{ at }}\omega =1\\&H(s)H(-s)={\frac {225}{-s^{6}+6s^{4}-45^{2}s+225}}\\&P(s)=225-B_{arith}^{2}(-s^{6}+6s^{4}-45^{2}s+225)=0.01S^{6}-0.06S^{4}+0.45S^{2}+222.75{\text{ (polynomial to be factored)}}\\&R=j5.0771344{\text{ (the positive imaginary root for the above polynomial)}}\\&text{forevenorderBesselfilters,usethepositiverealroot}\\&\omega _{-20dB{\text{ atten}}}=\omega _{c}=5.0771344{\text{ rad/sec (20dB attenuation frequency)}}\\&H(s)'=H(s)_{A=20dB{\text{ at }}\omega =1}={\frac {15}{(5.0771344^{3})s^{3}+(6*5.0771344^{2})s^{2}+(15*5.0771344)s+15}}\\&={\frac {15}{130.87478s^{3}+154.66376s^{2}+76.157016s+15}}\\&\\&{\text{Check:}}\\&|H(j)'|={\bigg |}{\frac {15}{130.87478j^{3}+154.66376j^{2}+76.157016j+15}}{\bigg |}=0.1=-20dB{\text{ Gain}}\end{aligned}}$

Filter Design Process

Filter designs begin with a set of design requirements and end with a final optimized filter of desired topology. Filter design requirements generally consist of pass band attenuation, stop band attenuation, pass band frequency, stop band frequency, and group delay. Some requirements may include cut-off frequencies to be different that the pass band frequency. Once a set of design requirements is defined, they are used as input parameters to design the final filter.

Classical filter design

Classical filter designs are a category of designs that may be implemented from Characteristic polynomials generally refereed to as $K(s)$ that embody the reflection zeros, frequencies where 100% transmission occurs, of the filter in the numerator and the transmission zeros, frequencies where no transmission occurs, in the denominator. The magnitude of $K(s)$ is normalized such that $|K(j)|=1$. Reflection and transmission zeros may be real, imaginary, complex, 0 or $\infty$. Imaginary transmission zeros are generally used to filter out specific undesired frequencies. Real and complex transmission zeros may be used to shape the group delay into a more desirable form. Any classical filter may be designed directly with the use of $K(s)$. However, this design method involves the use to root finding, and may not necessarily be the most efficient means to design a classical filter in many cases. Butterworth, Chebyshev, Inverse Chebyshev, and Elliptic filters are all classical filters that may be designed directly with classical design techniques.

The mathematical definition of $K(s)$ is as follows:

${\begin{aligned}&K(s)={\frac {\prod _{i=1}^{N_{r}}(s-r_{i})}{\prod _{i=1}^{N_{t}}(s-t_{i})}}\\&|K(s)|=1{\text{ at }}s=j\\&r_{i}{\text{are the reflection zeros}}\\&t_{i}{\text{are the transmission zeros}}\\\end{aligned}}$

Reflection zeros and transmission zero at $\infty$ are omitted from the expression above. For example, a five pole Butterworth filter has five reflection zeros at 0 and five transmission zeros at $\infty$. for this filter, $K(s)$ is simply $s^{5}$. If the Butterworth has a stop band zero at 2 rad/sec, $K(s)$ would be ${\frac {3s^{5}}{s^{2}+4}}$. The addition of "3" to the numerator meets the requirement that $|K(j)|=1$. A low pass all-pole (no finite transmission zeros) Chebyshev filter has its reflection zeros at the imaginary Chebyshev nodes and all transmission zeros at infinity, so a Chebyshev $K(s)$ would be the Hurwitz (all left half plane roots) Chebyshev polynomial.

The minimum size of the filter, set by variable N in the expression, is determined mathematically using topology dependent equations, or experimentally if no equations are known to exist.

Classical related design

Some filter designs, such as Legendre and Gaussian filters, are not designed explicitly with a $K(s)$ as defined above, but embody $K(s)$ style polynomials. For example, the $L_{N}(\omega ^{2})$ in the Legendre page may be expressed in the form of $K(s)K(-s)$. The denominator of $F_{N}(j\omega )$ in the Gaussian filter page may be expressed as $1+\varepsilon ^{2}K(s)K(-s)$, which embodies a $K(s)$ term. Both of these expressions may be used in the classical design process.

Nonclassical design

Other filter designs, such as Bessel filters, are designed directly on the transfer function, $G(s)$, without any interim process resembling a $K(s)$.

Obtaining the transfer function, G(s)

For the classical and related filter designs, the square of the transfer function is obtained from the expression below using the design pass band attenuation in dB..

${\begin{aligned}G(s)G(-s)&={\frac {1}{1+\varepsilon ^{2}K(s)K(-s)}}={\frac {K_{den}(s)K_{den}(-s)}{K_{den}(s)K_{den}(-s)+\varepsilon ^{2}K_{num}(s)K_{num}(-s)}}\\\varepsilon ^{2}&=10^{A_{p}/10}-1\\A_{p}&{\text{ is the pass band attenuation}}\\\end{aligned}}$

It can be seen from the expression above that the poles of $K(s)$ define the transmission zeros of $G(s)$, the frequencies where $|G(s)|=0$, and the zeros of $K(s)$ define the reflection zeros of $G(s)$, the frequencies where $|G(s)|=1$, with $\varepsilon$ as an interim variable used to set the pass band attenuation. It may also be seen in the expression above that a typical 3dB pass band attenuation results in an $\varepsilon ^{2}=0.99526231\approx 1$, which is usually close enough to simply eliminate $\varepsilon ^{2}$ from the expression when the pass band attenuation is designed to be 3dB.

$G(s)G(-s)$ is a ratio of even polynomials. That is, all zeros and poles of $G(s)G(-s)$ contain an equal and signed opposite zero and pole. To extract $G(s)$ from $G(s)G(-s)$, all opposing signed pairs of zeros and poles need to be found and one of the paired entries needs to be eliminated. For the $G(s)$ poles, only the $G(s)G(-s)$ poles with negative real values should be retained for the denominator of $G(s)$, creating a Hurwitz polynomial composed of only left half plane poles. The numerator of $G(s)$ may contain positive real values, so determining which zero to remove may be subjective and driven by the application, within the constraint that all zeros with an imaginary component retain their respective conjugate. Frequently, it is simply a matter of eliminating repeating pairs of zeros for the $G(s)$ numerator. Since $G(s)$ is ultimately derived from polynomials constructed from roots, it is generally necessary to magnitude scale $G(s)$ to retain $|G(s)|=1$ at the reflection zeros.

Nonstandard cut-off attenuation

The classical design equations assume the pass band edge occurs at the cut-off frequency, which works fine for maximally flat functions such as Butterworth and Inverse Chebyshev. However, functions such as Chebyshev and Legendre that have specific shapes associated with the pass band are problematic in that the design attenuation at the cutoff frequency is not necessarily the same as the design attenuation of the pass band. For example, Chebyshev designs for 0.05 dB pass band attenuation and -3 dB cut-off frequency attenuation are common. Although Chebyshev filters have an algebraic means to set the cutoff attenuation, other filter typologies such as Legendre may not. Therefore, a method is needed to universally set the cut-off attenuation for any filter topology.

Setting the cut-off attenuation frequency involves first finding the frequency that achieves the desired attenuation, which will be referred to as $\omega _{c}$, and then scaling either the $G(s)$ polynomials or the final filter design to the inverse of that frequency. If $K(s)$ is to be used as the reflection coefficient (see paragraph below), then $K(s)$ will also need to be inversely scaled. To scale the polynomials, simply append $\omega _{c}$ to the $s$ term in each coefficient, as shown in the 3 pole Bessel filter example below.

${\begin{aligned}G(s)&={\frac {15}{s^{3}+6s^{2}+15s+15}}\\G(s)'&=G(s)_{{\text{desired dB at }}\omega =1}={\frac {15}{(\omega _{c}s)^{3}+6(\omega _{c}s)^{2}+15\omega _{c}s+15}}\\\end{aligned}}$

$\omega _{c}$ may be found with Newton's method, or with root finding.

Finding attenuation frequency with Newton's method

Newton's method requires a known magnitude value and derivative magnitude value for the for $|G(j\omega _{c})|$. However, it is easier to operate on $|G(j\omega _{c})G(-j\omega _{c})|$ and use the square of the desired cutoff gain, and is just as accurate, so the square terms will be used.

To obtain $\omega _{c}$, follow the steps below.

1. If $G(s)G(-s)$ is not already available, multiply $G(s)$ by $G(-s)$ to obtain $G(s)G(-s)$.
2. negate all terms of $s^{n}$ when $(n+2)$ is divisible by $4$. That would be $s^{2}$, $s^{6}$, $s^{10}$, and so on. The modified function will be called $G_{2}(s)G_{2}(-s)$, and this modification will allow the use of real numbers instead of complex numbers when evaluating the polynomial and its derivative. the real $\omega _{a}$can now be used in place of the complex $j\omega _{a}$
3. Convert the desired attenuation in dB, $A_{dB}$, to a squared arithmetic gain value, $B_{arith}^{2}$, by using $B_{arith}^{2}=10^{A_{dB}/10}$. For example, 3.010 dB converts to 0.5, 1 dB converts to 0.79432823 and so on.
4. Calculate the modified $|G_{2}(s)G_{2}(-s)|$ in Newton's method using the real value, $\omega _{a}$. Always take the absolute value.
5. Calculate the derivative the modified $G_{2}(\omega _{a})G_{2}(-\omega _{a})$ with respect to the real value, $\omega _{a}$. DO NOT take the absolute value of the derivative.

When steps 1) through 4) are complete, the expression involving Newton's method may be written as:

$\omega _{a}=\omega _{a}-([G_{2}(\omega _{a})G_{2}(-\omega _{a})|-B^{2})/(d[G_{2}(\omega _{a})G_{2}(-\omega _{a})]/d\omega _{a})$

using a real value for $\omega _{a}$with no complex arithmetic needed. The movement of $\omega _{a}$ should be limited to prevent it from going negative early in the iterations for increased reliability. When complete, $\omega _{a}$ can used for the $\omega _{c}$ that can be used to scale the original $G(s)$ transfer function denominator. The attenuation of the modified $G(s)$ will then be virtually the exact desired value at 1 rad/sec. If performed properly, only a handful of iterations are needed to set the attenuation through a wide range of desired attenuation values for both small and very large order filters.

Finding attenuation frequency from the roots

Since $|G(j\omega _{a})|$ does not contain any phase information, directly factoring the transfer function will not produce usable results. However, the transfer function may be modified by multiplying it with $G(-s)$ to eliminate all odd powers of $G(j\omega a)$, which in turn forces $G(j\omega a)$ to be real at all frequencies, and then finding the frequency that result on the square of the desired attention.

1. If $G(s)G(-s)$ is not already available, multiply $G(s)$ by $G(-s)$ to obtain $G(s)G(-s)$.
2. Convert the desired attenuation in dB, $A_{dB}$, to a squared arithmetic gain value, $B_{arith}^{2}$, by using $B_{arith}^{2}=10^{A_{dB}/10}$. For example, 3.010 dB converts to 0.5, 1 dB converts to 0.79432823 and so on.
3. Find $P(S)=G_{num}(S)G_{num}(-S)-B_{arith}^{2}G_{den}(S)G_{den}(-S)$
4. Find the roots of P(S) using a root finding algorithm.
5. Of the set of roots from above, select the positive imaginary root for off order filters, and positive real root for even order filters.
   1. Cutoff attenuations that are above the pass band ripple or below the stop band ripple will come back with multiple roots, so the correct root will have to be selected.

Obtaining the reflection coefficient, R(s)

for doubly terminated networks, networks with a finite resistive termination at both ends, the reflection coefficient, $\rho (s)$, is usually needed to synthesize the network. $\rho (s)$ is obtainable from the network transfer function $T(s)$, where $T(S)={\frac {R_{2}}{R_{1}+R_{2}}}G(S)$, and $R_{1}$ and $R_{2}$ are the input and output termination resistances respectively. For simplicity, $R_{2}$ may be normalized to 1, yielding $T(S)={\frac {1}{R_{1}+1}}G(S)$, and then the synthesized network may be denormalized later by impedance scaling.

$\rho (s)$ may be derived with use of two-port network scattering parameter theory, namely taking advantage of the relations below.

${\begin{aligned}&|s_{11}|^{2}+|s_{12}|^{2}=1\\&S_{12}=2{\sqrt {\frac {R_{1}}{R_{2}}}}T(s)\\&S_{12}=2{\sqrt {R_{1}}}T(s)\\\\&T(S)={\frac {1}{R_{1}+1}}G(S)\\&R_{2}{\text{ is normalized to 1}}\\\end{aligned}}$

Since $\rho (s)$ is $s_{11}$, the deriving expression for $\rho (s)$ for normalized $R_{2}$ is below.

$\rho (s)\rho (-s)=1-4R_{1}T(s)T(-s)={\frac {T(s)_{den}T(-s)_{den}-4R_{1}T(s)_{num}T(-s)_{num}}{T(s)_{den}T(-s)_{den}}}$

Since the denominator of $T(s)$ is already known, only the numerator need be reconstructed, as shown.

$\rho (s)={\frac {\sqrt {T(s)_{den}T(-s)_{den}-4R_{1}T(s)_{num}T(-s)_{num}}}{T(s)_{den}}}$

zeros selection to obtain $\rho (s)_{num}$ from $\rho (s)_{num}\rho (-s)_{num}$ follows the same guidelines as those for $K(s)$ above.

The special case where $R_{1}=1$ simplifies $\rho (s)$ substantially in that $\rho (s)_{num}$ reduces to $K(s)_{num}$. For design cases where $R_{1}=1$ and $K(s)$ is already known, $K(s)_{num}$ may be directly substituted for $\rho (s)_{num}$ and then $\rho (s)$ simplifies to the following:

${\begin{aligned}&\rho (s)={\frac {K(s)_{num}}{G(s)_{den}}}\\\end{aligned}}$

When $R_{1}=1{\text{ and }}K(s){\text{ is known}}$

Obtaining the driving point impedance

The driving point impedance, $Z_{j}(s)$, the network impedance seen from the $R_{j}$ port, may be calculated directly from $\rho _{j}(s)$ for doubly terminated networks, and may be calculated directly from $G(s)$ for singly terminated networks.

Doubly terminated networks

Doubly terminated networks are networks with finite termination resistances at both ports. For these networks, $Z_{1}(s)$ may be found with algebraic manipulation of the following well known relation:

$\rho _{j}(s)=s_{jj}(s)={\frac {Z_{j}(s)-R_{j}}{Z_{j}(s)+R_{j}}}$

Algebraic manipulation yields the following relation:

$Z_{j}(s)=R_{j}{\frac {1+\rho _{j}(s)}{1-\rho _{j}(s)}}$

To insure that the final $R_{2}$ remains normalized to 1, and for simplicity reasons, the driving point impedance is taken from port 2, which effectively drops $R_{j}$ from the expression above, and the network synthesis process will calculate $R_{1}$ as the last element, which in some cases is not assured to be the same as the design $R_{1}$. This translation is permissible because $|\rho _{1}|=|\rho _{2}|$. The final expression for the driving point impedance, $Z_{in}$, used to synthesize the network is then as follows, with $\rho (s)$ being computed from $T(s)$ shown above.

$Z_{in}(s)={\frac {1+\rho (s)}{1-\rho (s)}}={\frac {\rho _{den}(s)+\rho _{num}(s)}{\rho _{den}(s)-\rho _{num}(s)}}$

Singly terminated networks

Singly terminated networks are networks with no resistive termination at the source. For even order singly terminated networks, $Z_{in}(s)$ may be found by the following relation, where "even" and "odd" suffixes refer to the even and odd coefficients of the polynomial, respectively:

$Z_{in}(s)={\frac {G_{den}(s)_{even}}{G_{den}(s)_{odd}}}$

for odd order networks, $Z_{dps}(s)$ may be found by the following:

$Z_{in}(s)={\frac {G_{den}(s)_{odd}}{G_{den}(s)_{even}}}$

Obtaining the network parameters

For some passive network applications, such as coupling matrix synthesis, it is useful to know the Z parameters, and/or Y parameters of the designed network. When needed, these parameters may be extracted from $Zin(s)$ through Darlington's method without the need to synthesize the network.

Final filter designs

For passive networks, the final frequency and impedance normalized filter design elements may be found through network synthesis from the driving point impedance of port 2. The first element extracted will be attached to port 2, and the final element for singly terminated networks will be attached to port 1. The final element extracted from doubly terminated networks will be the port 1 termination resistance, $R_{1}$. Some networks contain a transformative step up or step down, and will result in a termination source resistance other than the design $R_{1}$. When this happens, a Norton capacitor or inductor transformer or coupled coil transformer will have to be installed, or the calculated $R_{1}$ will have to be substituted for the design $R_{1}$. The normalized design may be converted to a final design by denormalizing both the impedance and frequency.

Some active filters typologies, such as Sallen and Key, MFB, Tow-Thomas, and GIC, are synthesized directly on the $G(s)$ polynomials followed by denormalization of the impedance and frequency. Other active filters simulate the corresponding normalized passive network, such as leapfrog and FDNR typologies followed by denormalization.

Digital filters may be synthesized from $G(s)$ and the desired sample rate using digital transformations such as bilinear transform, impulse invariance, or other desired digital transformation.

/////////////////////////////////////////////////////////////////////////////////////////////

Elliptic

Even order modifications

Even order Elliptic filters implemented with passive elements, typically inductors, capacitors, and transmission lines, with terminations of equal value on each side cannot be implemented with the traditional Elliptic transfer function without the use of coupled coils, which may not be desirable or feasible. This is due to the physical inability to accommodate the even order Chebyshev reflection zeros and transmission zeros that result in the scattering matrix S12 values that exceed the S12 value at $\omega =0$, and the finite S12 values that exist at $\omega =\infty$. If it is not feasible to design the filter with one of the terminations increased or decreased to accommodate the pass band S12, then the Elliptic transfer function must be modified so as to move the lowest even order reflection zero to $\omega =0$ and the highest even order transmission zero to $\omega =\infty$ while maintaining the equi-ripple response of the pass band and stop band.

The needed modification involves mapping each pole and zero of the Elliptic transfer function in a manner that maps the lowest frequency reflection zero to zero, the highest frequency transmission zero to $\infty$, and and the remaining poles and zeros as needed to maintain the equi-ripple pass band and stop band. The lowest frequency reflection zero may be found by factoring the $K(s)$ numerator, and the highest frequency transmission zero may be found be factoring the $K(s)$ denominator.

The translate the reflection zeros, the following equation is applied to all poles and zeros of $K(s)$. While in theory, the translation operations may be performed on either $K(s)$ or $G(s)$, the reflection zeros must be extracted from $K(s)$, so it is generally more efficient to perform the translation operations on $K(s)$.

$R_{i}'={\sqrt {\frac {R_{i}^{2}+\omega _{LO}^{2}}{1-\omega _{LO}^{2}}}}$

Where:

$R_{i}$ is the original Elliptic function zero or pole

$R_{i}'$ is the mapped zero or pole for the modified even order transfer function.

$\omega _{LO}$ is the lowest frequency reflection zero in the pass band.

The sign of imaginary component of $R_{i}'$ is determined by the sign of the original $R_{i}$.

The translate the transmission zeros, the following equation is applied to all poles and zeros of $K(s)$. While in theory, the translation operations may be performed on either $K(s)$ or $G(s)$, if the reflection zeros must be extracted from $K(s)$, it may be more efficient to perform the translation operations on $K(s)$.

$R_{i}'={\sqrt {\frac {(\omega _{HI}^{2}-1)R_{i}^{2}}{\omega _{HI}^{2}+R_{i}^{2}}}}$

Where:

$R_{i}$ is the original Elliptic function zero or pole

$R_{i}'$ is the mapped zero or pole for the modified even order transfer function.

$\omega _{HI}$ is the highest frequency transmission zero in the pass band.

The sign of imaginary component of $R_{i}'$ is determined by the sign of the original $R_{i}$. If operating on $G(s)$ the sign of the real component of $R_{i}'$ must be negative to conform to the left half plane requirement.

It is important to note that all applications require both pass and and stop translations. Passive network diplexers, for example, only require even order stop band translations, and perform more efficiently with untranslated even order pass bands.

When $G(s)$ is completed, an equi-ripple transfer function is created with scattering matrix values for S12 of 1 $\omega =0$ and 0 at $\omega =\infty$, which may be implements with passive equally terminated networks.

The illustration below shows an 8th order Elliptic filter modified to support even order equally terminated passive networks by relocating the lowest frequency reflection zero from a finite frequency to 0 and the highest frequency transmission zero to $\infty$ while maintaining an equi-ripple pass band and stop band frequency response.

Even order modified Elliptic illustration

The $\Omega _{c}$ and order computation in the Elliptic construction paragraph above are for unmodified Elliptic filters only. Although even order modifications have no effect on the pass band or stop band attenuation, small errors are to be expected in the order and $\Omega _{c}$ computations. Therefore, it is important to apply even order modifications after all $K(s)$ iterations complete if it is desired to preserve the pass and stop band attenuations. If the even order modified Elliptic function is created from an $\Omega _{c}$requirement, the actual $\Omega _{c}$ will be slightly larger than the design $\Omega _{c}$. Likewise, an order, n, computation may result in a smaller value than the actual required order.

Construction from Chebyshev transmission zeros

Elliptic filter stop bands are essentially Chebyshev filters with transmission zeros where the transmission zeros are arranged in a manner that yields an equi-ripple stop band. Given this, it is possible to convert a Chebyshev filter characteristic equation, $K(s)$ containing the Chebyshev reflection zeros in the numerator and no transmission zeros in the denominator, to an Elliptic filter $K(s)$ containing the Elliptic reflection zeros in the numerator and Elliptic transmission zeros in the denominator, by iteratively creating transmission zeros from the scaled inverse of the Chebyshev reflection zeros, and then reestablishing an equi-ripple Chebyshev pass band from the transmission zeros, and repeating until the iterations produce no further changes of significance to $K(s)$. The scaling factor used, $\Omega _{c}$, is the stop band to pass band cutoff frequency ratios and is also known as the inverse of the "selectivity factor". Since Elliptic designs are generally specified from the stop band attenuation requirements, $\Omega _{c}$, may be derived from the equations that establish the minimum order, n, for given stop and pass band attenuation and frequency requirements.

${\begin{aligned}{\text{Given:}}&\\A_{p}&={\text{ pass band ripple in dB}}\\A_{s}&={\text{ stop band ripple in dB}}\\\omega _{p}&={\text{ maximum pass band frequency}}\\\omega _{s}&={\text{ minimun stop band frequency}}\\D&={\frac {10^{A_{s}/10}-1}{10^{A_{p}/10}-1}}\\\\{\text{Then:}}&\\k&={\text{ the selectivity factor }}={\frac {\omega _{p}}{\omega _{s}}}\\u&={\frac {1-{\sqrt[{4}]{1-k^{2}}}}{2(1+{\sqrt[{4}]{1-k^{2}}})}}\\q&=u+2u^{5}+15u^{9}+150u^{13}\\D&={\frac {10^{A_{s}/10}-1}{10^{A_{p}/10}-1}}\\n&={\text{ minimum order }}=ceil{\bigg (}{\frac {\log {16D}}{\log(1/q)}}{\bigg )}\\\end{aligned}}$

the $\omega _{s}/\omega _{p}$ ratio, $\Omega _{c}$ may be derived by working the problem above backwards from n to find $\Omega _{c}$.

${\begin{aligned}q&=(16D)^{(-1/n)}\\0&=-q+u+2u^{5}+15u^{9}+150u^{13}\\u&={\text{ real root of above equation}}\\k&={\text{ the selectivity factor }}={\sqrt {1-{\bigg (}{\frac {1-2u}{1+2u}}{\bigg )}^{4}}}\\\Omega _{c}&={\frac {\omega _{s}}{\omega _{p}}}={\frac {1}{k}}={\frac {1}{\sqrt {1-{\bigg (}{\frac {1-2u}{1+2u}}{\bigg )}^{4}}}}\\\end{aligned}}$

The characteristic polynomials, $K(s)$, may then be translated to the transfer function polynomials, $G(s)$ with the classic translation, $G(s)={\sqrt {1/(1+\varepsilon ^{2}K(s)K(-s))}}{\bigg |}_{\text{LHP poles}}$ where $\varepsilon ^{2}=10^{Ap/10.}-1.$ and $A_{p}$ is the pass band ripple.

Simple example

Design an Elliptic filter with a pass band ripple of 1 dB from 0 to 1 rad/sec and a stop band ripple of 40 dB from at least 1.25 rad/sec to $\infty$.

Applying the calculations above for the value for n prior to applying the ceil() function, n is found to be 4.83721900 rounded up to the next integer, 5, by applying the ceil() function, which means a 5 pole Elliptic filter is required to meet the specified design requirements. Applying the calculations above for $\Omega _{c}$ needed to design a stop band of exactly 40dB of attenuation, $\Omega _{c}$ is found to be 1.2186824.

The polynomial scaled inversion function may be performed by translating each root, s, to $\Omega _{c}/s$, which may be easily accomplished by inverting the polynomial and scaling it by $\Omega _{c}$, as shown.

${\begin{aligned}&as^{n}+bs^{n-1}\dots cs^{2}+ds^{1}+es^{0}\Longrightarrow ({\frac {e}{\Omega _{c}^{n}}})s^{n}+({\frac {d}{\Omega _{c}^{n-1}}})s^{n-1}\dots ({\frac {c}{\Omega _{c}^{2}}})s^{2}+({\frac {b}{\Omega _{c}^{1}}})s^{1}+({\frac {a}{\Omega _{c}^{0}}})s^{0}\\\end{aligned}}$

The Elliptic design steps are then as follows:

1. Design a Chebyshev filters with 1 dB pass band ripple.
2. Invert all the reflections zeros about $\Omega _{c}$to create transmission zeros
3. Create an equi-ripple pass band from the transmission zeros using the process outlined is Chebyshev transmission zeros
4. Repeat steps 2 and 3 until both the pass band and stop band no longer change by any appreciable amount. Typically, 15 to 25 iterations produce coefficient differences in the order of than 1.e-15.

To illustrate the steps, the below K(s) equations begin with a standard Chebyshev K(s), then iterate through the process. Visible differences are seen in the first three iterations. By time 18 iterations have been reached, the differences in K(s) become negligible. Iterations may be discontinued when the change in K(s) coefficients becomes sufficiently small so as to meet design accuracy requirements. The below K(s) iterations have all been normalized such that $|K(j)|=1$, however, this step may be postponed until the last iteration, if desired.

${\begin{aligned}{\text{iteration 0: }}K(s)&={\frac {16s^{5}+20s^{3}+5s}{1}}\\{\text{iteration 1: }}K(s)&={\frac {9.2965947s^{5}+12.999133s^{3}+4.0025668s}{0.14167325s^{4}+0.84164496s^{2}+1}}\\{\text{iteration 2: }}K(s)&={\frac {8.6496472s^{5}+12.270597s^{3}+3.8746611s}{0.19518773s^{4}+0.94147634s^{2}+1}}\\&\vdots \\{\text{iteration 17: }}K(s)&={\frac {8.550086786383502s^{5}+12.157269873073034s^{3}+3.854163602012615s}{0.2043607336740334s^{4}+0.9573802183509494s^{2}+1}}\\{\text{iteration 18: }}K(s)&={\frac {8.550086786383422s^{5}+12.157269873072942s^{3}+3.854163602012599s}{0.2043607336740334s^{4}+0.9573802183509494s^{2}+1}}\\\end{aligned}}$

To find the $G(s)$ transfer function, do the following.

${\begin{aligned}\varepsilon ^{2}&=10^{1dB/10.}-1.=.25892541\\G(s)&={\sqrt {G(s)G(-s)}}{\bigg |}_{\text{LHP poles}}={\sqrt {\frac {1}{1+\varepsilon ^{2}K(s)K(-s)}}}{\bigg |}_{\text{LHP poles}}={\sqrt {\frac {K(s)_{den}K(-s)_{den}}{K(s)_{den}K(-s)_{den}+\varepsilon ^{2}K(s)_{num}K(-s)_{num}}}}{\bigg |}_{\text{LHP poles}}\\&={\frac {0.20436073s^{4}+0.95738022s^{2}+1}{{\sqrt {-18.928479s^{10}-53.78661s^{8}-54.942632s^{6}-22.939175s^{4}-1.931467+1}}{\bigg |}_{\text{LHP poles}}}}\\\end{aligned}}$

To obtain $G(s)$ from the left half plane, factor the numerator and denominator to obtain the roots using a root finding algorithm. Discard all roots from the right half plane of the denominator, half the repeated roots in the numerator, and rebuild $G(s)$ with the remaining roots. Generally, normalize $|G(s)|$ to 1 at $s=0$.

${\begin{aligned}&G(s)={\frac {0.20436073s^{4}+0.95738022s^{2}+1}{4.3506872s^{5}+4.0174213s^{4}+8.0362343s^{3}+4.9129149s^{2}+3.4288915s+1}}\\\end{aligned}}$

To confirm that the example $G(s)$ is correct, the plot of $G(s)$ along $j\omega$ is shown below with a pass band ripple of 1 dB, a cut off frequency of 1 rad/sec, a stop band attenuation of 40 dB beginning at 1.21868 rad/sec

Five pole Elliptic simulation

Reflection Zeros

For any given transfer function, frequencies may exist where the reflection coefficient is zero. This condition is achieved with an ideal lossless network that transmits all of the energy to the load, or with ideal lossy passive networks that transmit all of the energy to internal lossy elements. Reflection zeros may occur at infinite frequency, 0 frequency, or finite frequencies. Finite frequency reflection zeros typically show up in the network frequency response as humps with peaks of 1 or 0dB Reflection zeros at 0 frequency occur with low pass filters and band stop filters. Reflection zeros at infinity typically occur with high pass filters and band pass filters. Finite frequency reflection zeros typically show up with Chebyshev filters and Elliptic filters.

InvChebyshev even order:

The illustration below shows an 8th order Inverse Chebyshev filter modified to support even order equally terminated passive networks by relocating the highest frequency transmission zero from a finite frequency to $\infty$ while maintaining an equi-ripple stop band frequency response.

Even order modified Inverse Chebyshev illustration

Even order modifications

Even order Chebyshev filters implemented with passive elements, typically inductors, capacitors, and transmission lines, with terminations of equal value on each side cannot be implemented with the traditional Chebyshev transfer function. This is due to the physical inability to accommodate the even order Chebyshev reflection zeros that result in a scattering matrix S12 values that exceed the S12 value at $\omega =0$. If it is not feasible to design the filter with one of the terminations increased or decreased to accommodate the pass band S12, then the Chebyshev transfer function must be modified so as to move the lowest even order reflection zero to $\omega =0$ while maintaining the equi-ripple response of the pass band.

The needed modification involves mapping each pole of the Chebyshev transfer function in a manner that maps the lowest frequency reflection zero to zero and the remaining poles as needed to maintain the equi-ripple pass band. The lowest frequency reflection zero may be found from the Chebyshev Nodes, $cos{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}$. The complete Chebyshev pole mapping function is shown below.

$P'=\left[{\sqrt {\left({\frac {P^{2}+cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}{1-{cos^{2}{\Bigl (}{\frac {\pi (n-1)}{2n}}{\Bigl )}}}}\right)}}\right]_{\text{Left Half Plane }}$

Where:

n is the order of the filter (must be even)

P is a traditional Chebyshev transfer function pole

P' is the mapped pole for the modified even order transfer function.

"Left Half Plane" indicates to use the square root containing a negative real value.

When complete, a replacement equi-ripple transfer function is created with reflection zero scattering matrix values for S12 of one and S11 of zero when implemented with equally terminated passive networks. The illustration below shows an 8th order Chebyshev filter modified to support even order equally terminated passive networks by relocating the lowest frequency reflection zero from a finite frequency to 0 while maintaining an equi-ripple pass band frequency response.

Even order modified Chebyshev illustration

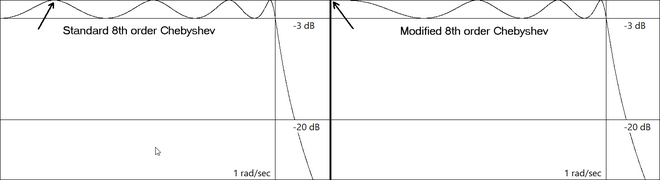
The LC element value formulas in the Cauer topology are not applicable to the even order modified Chebyshev transfer function, and cannot be used. It is therefore necessary to calculate the LC values from traditional continued fractions of the impedance function, which may be derived from the reflection coefficient, which in turn may be derived from the transfer function.

Asymmetric band pass

Chebyshev band pass filters may be designed with a geometrically asymmetric frequency response by placing the desired number of transmission zeros at zero and infinity with the use of the more generalized form of the Chebyshev transmission zeros equation above, and shown below. The $K(s)$ equations below consider a frequency normalized pass band from 1 to $\omega _{2}$. If the number of transmission zeros at 0 is not the same as the number of transmission zeros at $\infty$, the filter will be geometrically asymmetric. The filter will also be asymmetric if finite transmission zeros are not place symmetrically about the geometric center frequency, which in this case is ${\sqrt {\omega _{2}}}$. There is a restriction in that he filter must be net even order, that is the sum of all the poles must be even, to make the asymmetric $K(s)$ equation produce usable results. Real and complex quadruplet transmission zeros may also be created using this technique and are useful to modify the group delay response, just as in the low pass case. The derivation of the characteristic equation, $K(s)$, to create an asymmetric Chebyshev band pass filter is shown below.

${\begin{aligned}K(s)&={\frac {{\bigg \{}\prod _{i=1}^{N}{\bigg (}M_{i}{\sqrt {s^{2}+\omega _{2}^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg \}}_{\text{rational term only}}}{s^{N_{z}}\prod _{i=1}^{N_{f}}(1-s/z_{i})}}\\M_{i}&={\sqrt {\frac {z_{i}^{2}+1}{z_{i}^{2}+\omega _{2}^{2}}}}{\text{ for }}\sigma _{i}\neq 0{\text{ or }}\omega _{i}<1{\text{ or }}\omega _{i}>\omega _{2}\\&={\sqrt {\frac {1-\omega _{i}^{2}}{\omega _{2}^{2}-\omega _{i}^{2}}}}{\text{ for }}\sigma _{i}=0{\text{ and }}0<\omega _{i}<1\\&={\sqrt {\frac {\omega _{i}^{2}-1}{\omega _{i}^{2}-\omega _{2}^{2}}}}{\text{ for }}\sigma _{i}=0{\text{ and }}\omega _{2}<\omega _{i}<\infty \\&={\frac {1}{\omega _{2}}}{\text{ for }}z_{i}=0\\&=1{\text{ for }}z_{i}=\infty \\N_{z}&={\text{ number of transmission zeros at zero}}\\N_{f}&={\text{ number of finite transmission zeros (imaginay, real, and complex)}}\\z_{i}&=\sigma _{i}+j\omega _{i}={\text{ complex transmision zero}}\\\omega _{2}&={\text{ upper passband corner frequency (lower corner is normalized to 1)}}\\\end{aligned}}$

$K(s)$ should be normalized such that $|K(s)|=1{\text{ at }}s=j$, if needed.

Simple example

Design an asymmetric Chebyshev filter with 1dB pass band ripple from 1 to 2 rad/sec, one transmission zero at $\infty$, and three transmission zeros at 0. By applying the numeral values to the equations above, the characteristic polynomials, $K(s)$, may be calculated as follows.

${\begin{aligned}\omega _{2}&=2\\M_{1}&=M_{2}=M_{3}=.5\\M_{4}&=1\\K(s)&={\frac {{\bigg \{}{\bigg (}.5{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg (}.5{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg (}.5{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg (}{\sqrt {s^{2}+2^{2}}}+{\sqrt {s^{2}+1}}{\bigg )}{\bigg \}}_{\text{rational term only}}}{s^{3}}}\\K(s)&=C{\frac {3.375s^{4}+14.25s^{2}+12+{\sqrt {\dots }}}{s^{3}}}{\text{ where C is a constant used to normalize the magnitude to 1 at }}s=j\\\end{aligned}}$

Discarding the irrational part and normalizing $|K(s)|$ to 1 at s=j:

${\begin{aligned}K(s)&={\frac {3s^{4}+12.666667s^{2}+10.666667}{s^{3}}}\\\end{aligned}}$

Use the same process as in the low pass case to find $G(s)$ from $K(s)$, using constant $C$ to scale the magnitude.

${\begin{aligned}\varepsilon ^{2}&=10^{1dB/10.}-1.=.25892541\\G(s)&=C{\sqrt {\frac {K(s)_{den}K(-s)_{den}}{K(s)_{den}K(-s)_{den}+\varepsilon ^{2}K(s)_{num}K(-s)_{num}}}}{\bigg |}_{\text{LHP poles}}\\&=C{\frac {s^{3}}{{\sqrt {(s)^{3}(-s)^{3}+.25892541\{3(s)^{4}+12.666667(s)^{2}+10.666667\}\{3(-s)^{4}+12.666667(-s)^{2}+10.666667\}}}{\bigr |}_{\text{LHP poles}}}}\\&=C{\frac {s^{3}}{{\sqrt {2.3303287s^{8}+18.678331s^{6}+58.11437s^{4}+69.9674s^{2}+29.459958}}{\bigr |}_{\text{LHP poles}}}}\\\end{aligned}}$

When reconstructing the denominator from the left half plane poles, it will be necessary to set the $G(s)$ magnitude such that the reflection zeros occur at 0dB. To do this, $G(s)$ should be scaled such that $|G(s)|$ = -1dB at the pass band corner frequencies, $s=j$ and $s=j2$. Once accomplished, the final transfer function for the designed asymmetric Chebyshev filter is shown below.

${\begin{aligned}G(s)&={\frac {0.18424001s^{3}}{0.28125000s^{4}+0.34089984s^{3}+1.3337548s^{2}+0.54084155s+1}}\\\end{aligned}}$

Evaluating $|G(s)|$ at s=j and at s=2j produces a value of -1dB in both cases, yielding an assurance that the example has been synthesized correctly. The frequency response is below, showing a Chebyshev 1dB equi-ripple pass band response for $1<\omega <2$, cutoff attenuation of -1dB at the pass band edges, -60dB / decade attenuation toward $\omega =0$, -20dB / decade attenuation toward $\omega =\infty$, and Chebyshev style steepened slopes near the pass band edges.

Simulation showing asymmetric Chebyshev

Chebyshev transmission zeros

Chebyshev filters may be designed with arbitrarily placed finite transmission zeros in the stop band while retaining an equi-ripple pass band. Stop band zeros along the $j\omega$ axis are generally used to eliminate unwanted frequencies. Stop band zeros along the real axis or quadruplet stop band zeros in the complex plane may be used to modify the group delay to a more desirable shape. The transmission zeros design utilizes characteristic polynomials, K(S), to place the transmission and reflection zeros, which in turn are used to create the transfer function, $G(s)$,

$G(s)={\sqrt {\frac {1}{1+\varepsilon ^{2}K(s)K(-s)}}}{\bigg |}_{\text{left half plane (LHP) poles}}$

The calculation of K(S) relies upon the following observed equality.

${\begin{aligned}&{\begin{array}{lcr}&{\bigg |}\prod _{i=1}^{N}{\frac {j\omega {\frac {\sqrt {z_{i}^{2}+1}}{z_{i}}}+{\sqrt {1-\omega ^{2}}}}{(1-j\omega /z_{i})}}{\bigg |}=1.&&{\text{ for }}0\leq \omega \leq 1\end{array}}\\\end{aligned}}$

for all $z_{i}=\infty$, imaginary conjugate pairs, quadruplet conjugate pairs, or real opposing signed pairs.

Given the magnitude is always one in the pass bane ($0\leq \omega \leq 1$) the rational and irrational terms must vary between 0 and 1. Therefore, if only the rational term is used to create the $K(s)$ characteristic function, an equi-ripple response is expected in the pass band, and characteristic poles (transmission zeros) are expected at all $s=z_{i}$.

The design process for K(S) using the above expression is below.

${\begin{aligned}K(s)&={\frac {{\bigg \{}\prod _{i=1}^{N}{\bigg (}M_{i}s+{\sqrt {s^{2}+1}}{\bigg )}{\bigg \}}_{\text{rational term only}}}{\prod _{i=1}^{N}(1-s/z_{i})}}\\M_{i}&={\frac {\sqrt {z_{i}^{2}+1}}{z_{i}}}{\text{ for }}\sigma _{i}\neq 0{\text{ or }}\omega _{i}>1\\&={\frac {\sqrt {\omega _{i}^{2}-1}}{\omega _{i}}}{\text{ for }}\sigma _{i}=0{\text{ and }}\omega _{i}>1\\&=1{\text{ for }}\omega _{i}=\infty \\z_{i}&=\sigma _{i}+j\omega _{i}={\text{ complex transmision zero}}\\\end{aligned}}$

Use the positive $M_{i}$ solution for real and imaginary $z_{i}$ pairs. Use the positive real and conjugate imaginary $M_{i}$solution for complex $z_{i}$ pairs.

$K(s)$ should be normalized such that $|K(s)|=1{\text{ at }}s=j$, if needed.

The, "rational terms only" indicates to keep the rational part of the product, and to discard the irrational part. The rational term may be obtained by manually performing the polynomial arithmetic, or with the short cut below which is a solution derived from polynomial arithmetic and uses binomial coefficients.

${\begin{aligned}&B=\prod _{i=1}^{N}(M_{i}s+1)\\&K(s)_{num}=\sum _{i=N}^{i\geq 0{\text{, step }}=-2}{\bigg [}\sum _{j=i}^{j\geq 0{\text{, step }}=-2}B_{j}{\binom {(N-j)/2}{(N-i)/2}}{\bigg ]}s^{i}\\&N={\text{ order of the Chebyshev filter}}\\&B={\text{a polynomial created by the product of the specified factors}}\\&B_{j}={\text{ the }}j_{th}{\text{ order coefficent of polynomial }}B\\&{\binom {n}{k}}{\text{ is the binomial coefficient function}}\\\end{aligned}}$

When all M values are set to one, then $K(s)_{num}$ will be the standard Chebyshev equation, which is expected since the all transmission zeros are it $\infty$. It is also important to remember that even order finite transmission zero Chebyshev filters have the same limitation as the all-pole case in that they cannot be constructed using equally terminated passive networks. The same even order modification may be made to the even order characteristic polynomials, $K(s)$, to make equally terminated passive network implementations possible. However, the even order modification will also move the finite transmission zeros slightly. This movement may be significantly mitigated by propositioning the transmission zeros with the inverse of the even order modification using the lowest Chebyshev node, $cos(\pi (N-1)/(2N))$.

${\begin{aligned}&z_{i}'={\sqrt {z_{i}^{2}(1.-C_{0}^{2})-C_{0}^{2}}}\\&C_{0}^{2}=cos^{2}({\frac {\pi (N-1)}{2N}})\\&z_{i}={\text{desired finite transmisison zero}}\\&z_{i}'={\text{prepositioned finite transmisison zero}}\\\end{aligned}}$

Simple example

Design a 3 pole Chebyshev filter with a 1 dB pass band, a transmission zero at 2 rad/sec, and a transmission zero at $\infty$:

${\begin{aligned}&M_{1}=M_{2}={\sqrt {(j2)^{2}+1}}/j2={\sqrt {1-4}}/j2={\sqrt {3}}/2=0.866025{\text{, }}M_{3}={\sqrt {\infty ^{2}+1}}/\infty =1\\&\\&{\text{Full polynomial derivation:}}\\&K(s)_{num}={\bigr (}0.86602540s+{\sqrt {s^{2}+1}}{\bigr )}{\bigr (}0.86602540s+{\sqrt {s^{2}+1}}{\bigr )}{\bigr (}s+{\sqrt {s^{2}+1}}{\bigr )}\\&K(s)_{num}=3.4820508s^{3}+2.7320508s+{\sqrt {\dots }}\\&{\text{discarding the irrational }}{\sqrt {\dots }}{\text{ and keeping only the rational part:}}\\&K(s)_{num}=3.4820508s^{3}+2.7320508s\\&\\&K(s)_{num}{\text{ shortcut derivation:}}\\&B=(0.86602540s+1)(0.86602540s+1)(s+1)=.75s^{3}+2.4820508s^{2}+2.7320508s+1\\&K(s)_{num}={\bigg (}0.75{\binom {0}{0}}+2.4820508{\binom {1}{0}}{\bigg )}s^{3}+{\bigg (}2.7320508{\binom {1}{1}}{\bigg )}s\\&K(s)_{num}=3.4820508s^{3}+2.7320508s\\&\\&k(s)_{den}=({\frac {s}{j2}}+1)({\frac {s}{-j2}}+1)=0.25s^{2}+1\\&{\text{Check }}|K(s)|{\text{ at }}s=j{\text{ to insure it is unity, and adjust with a constant, if necessary:}}\\&{\bigg |}{\frac {K(s)_{num}(s=j)}{K(s)_{den}(s=j)}}{\bigg |}=1{\text{ Check!}}\\&K(s)={\frac {3.4820508s^{3}+2.7320508s}{0.25s^{2}+1}}\\\end{aligned}}$

To find the $G(s)$ transfer function, do the following.

${\begin{aligned}&\varepsilon ^{2}=10^{1dB/10.}-1.=.25892541\\&G(s)={\sqrt {G(s)G(-s)}}{\bigg |}_{\text{LHP poles}}={\sqrt {\frac {1}{1+\varepsilon ^{2}K(s)K(-s)}}}{\bigg |}_{\text{LHP poles}}={\sqrt {\frac {K(s)_{den}K(-s)_{den}}{K(s)_{den}K(-s)_{den}+\varepsilon ^{2}K(s)_{num}K(-s)_{num}}}}{\bigg |}_{\text{LHP poles}}\\&={\sqrt {\frac {\{0.25(s)^{2}+1\}\{{0.25(-s)^{2}+1}\}}{\{0.25(s)^{2}+1\}\{{0.25(-s)^{2}+1}\}+.25892541\{3.4820508(s)^{3}+2.7320508(s)\}\{3.4820508(-s)^{3}+2.7320508(-s)\}}}}{\bigg |}_{\text{LHP poles}}\\&={\frac {0.25(s)^{2}+1}{{\sqrt {-3.1393872s^{6}-4.8638872s^{4}-1.4326456s^{2}+1}}{\bigr |}_{\text{LHP poles}}}}\\\end{aligned}}$

To obtain $G(s)$ from the left half plane, factor the numerator and denominator to obtain the roots. Discard all roots from the right half plane of the denominator, half the repeated roots in the numerator, and rebuild $G(s)$ with the remaining roots. Generally, normalize $|G(s)|$ to 1 at $s=0$.

${\begin{aligned}&G(s)={\frac {0.25s^{2}+1}{1.7718316s^{3}+1.7200107s^{2}+2.2074118s+1}}\\\end{aligned}}$

To confirm that the example $G(s)$ is correct, the plot of $G(s)$ along $j\omega$ is shown below with a pass band ripple of 1 dB, a cut off frequency of 1 rad/sec, and a stop band zero at 2 rad/sec.

Chebyshev transmission zero at 2 rad/sec

Setting the cutoff attenuation

There is no standard set attenuation value for Bessel filters, however, −3.0103 dB is a common choice. Some applications may use a higher or lower attenuation, such as −1 dB or −20 dB. The attenuation is set by frequency scaling the denominator. This can be approximated by interpolating Bessel filter attenuation tables, or calculated precisely with Newton's method or a the use of a root finding algorithm.

The denominator may be frequency scaled by using a scaling factor that will be refered to as $\omega _{c}$. The frequency-scaled denominator of the Bessel transfer function may be rewritten for the $n=3$ case above and the example below as follows:

$H(s)'=H(s)_{{\text{desired dB at }}\omega =1}={\frac {15}{(s\omega _{c})^{3}+6(s\omega _{c})^{2}+15s\omega _{c}+15}}$

The task for modifying $H(s)$ is to find an $\omega _{c}$ that results in the desired attenuation at 1 r/s for the normalized transfer function. Newton's method can be summarized to do this by its basic definition:

$\omega _{a}=\omega _{a}+(|H(j\omega _{a})|-{\text{DesiredAttenuation}})/(d|H(j\omega _{a})|/dj\omega _{a})$

through successive iterations of $\omega _{a}$ until $\omega _{a}$is the frequency that attenuates $|H(j\omega _{a})|$ to the desired attenuation.

While the above summary may be concise and easily understood, the mechanics of obtaining an accurate derivative of the magnitude function along the $j\omega$ axis may be problematic. Digital techniques may be used, but it is generally better to apply analytical techniques with continuous functions, if possible, so as to maximize accuracy. $\omega _{a}$ may be determined by either of the following methods.

Finding attenuation frequency with Newton's method

Newton's method requires a known magnitude value and derivative magnitude value for the for $|H(j\omega a)|$. To obtain these values, make the following alterations:

1. Multiply $H(s)$ by $H(-s)$ to obtain $H(s)H(-s)$. This will eliminate complex numerical results when evaluating $|H(s)H(-s)|$ by removing the odd order terms in the polynomial.
2. In $H(s)H(-s)$, negate all terms of $s^{n}$ when $(n+2)$ is divisible by $4$. That would be $s^{2}$, $s^{6}$, $s^{10}$, and so on. We will call the modified function $H_{2}(s)H_{2}(-s)$, and this modification will allow the use of real numbers instead of complex numbers when evaluating the polynomial and its derivative. That is, we can now use the real $\omega _{a}$in place of the complex $j\omega _{a}$
3. Convert the desired attenuation in dB, $A_{dB}$, to an arithmetic attenuation value, $A_{arith}$, using $A_{arith}=10^{A_{dB}/20}$. For example, −3.010 dB is 0.7071, −1 dB is 0.8913 and so on. This simplifies the derivative evaluation.
4. Square the resulting arithmetic attenuation to correlate with the squaring of the $H(s)$ function.
5. Calculate the modified $[H_{2}(\omega _{a})H_{2}(-\omega _{a})]$ in Newton's method using the real value, $\omega _{a}$. Always take the absolute value.
6. Calculate the derivative the modified $H_{2}(\omega _{a})H_{2}(-\omega _{a})$ with respect to the real value, $\omega _{a}$. Negate the derivative computation to account for the effects due to the modifications made to create $H_{2}(\omega _{a})H_{2}(-\omega _{a})$. DO NOT take the absolute value of the derivative.

When steps 1) through 4) are complete, the expression involving Newton's method may be written:

$\omega _{a}=\omega _{a}+([H_{2}(\omega _{a})H_{2}(-\omega _{a})]-{\text{DesiredAttenuation}})/(d[H_{2}(\omega _{a})H_{2}(-\omega _{a})]/d\omega _{a})$

using a real value for $\omega _{a}$with no complex arithmetic needed. The movement of $\omega _{a}$ should be limited to prevent it from going negative early in the iterations for increased reliability. When complete, $\omega _{a}$ can used for the $\omega _{c}$ that can be used to scale the original $H(s)$ transfer function denominator. The attenuation of the modified $H(s)'$ will then be virtually the exact desired value at 1 rad/sec. If performed properly, only a handful of iterations are needed to set the attenuation through a wide range of desired attenuation values for both small and very large order Bessel filters.

Finding attenuation frequency from the roots

Since $|H(j\omega _{a})|$ does not contain any phase information, directly factoring the transfer function will not produce usable results. However, the transfer function may be modified by multiplying it with $H(-s)$ to eliminate all odd powers of $H(j\omega a)$, which in turn forces $H(j\omega a)$ to be real at all frequencies, and then finding the frequency that result on the square of the desired attention.

1. Multiply $H(s)$ by $H(-s)$ to obtain $H(s)H(-s)$.
2. Convert the desired attenuation in dB, $A_{dB}$, to a squared arithmetic attenuation value, $A_{arith}^{2}$, by using $A_{arith}^{2}=10^{A_{dB}/10}$.
3. Find $P(S)=H_{num}(S)H_{num}(-S)-A_{arith}^{2}H_{den}(S)H_{den}(-S)$
4. Find the roots of P(S) using a root finding algorithm.
5. Of the set of roots from above, there will be one and only one positive imaginary root for a function such as Bessel filters that continuously attenuates as frequency increases. The imaginary value of this root will be frequency that results in the desired attenuation, $\omega c$.

For example, setting the example 3rd order Bessel filter to -20dB at a cutoff frequency of 1 rad/sec is performed as follows:

${\begin{aligned}&A_{arith}^{2}=10^{-(-20)/10}=0.01\\&H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}\\&H(s)H(-s)={\frac {225}{-s^{6}+6s^{4}-45^{2}s+225}}\\&P(s)=225-0.01(-s^{6}+6s^{4}-45^{2}s+225)=0.01S^{6}--0.06S^{4}+0.45S+222.75\\&R_{positive,imaginary}=j5.0771344\\&\omega _{-20dB{\text{ atten}}}=\omega _{c}=5.0771344{\text{ rad/sec}}\\&H(s)'=H(s)_{-20dB{\text{ at }}\omega =1}={\frac {15}{(5.0771344^{3})s^{3}+(6*5.0771344^{2})s^{2}+(15*5.0771344)s+15}}\\&\\&{\text{Check:}}\\&|H(j)'|={\bigg |}{\frac {15}{(5.0771344^{3})j^{3}+(6*5.0771344^{2})j^{2}+(15*5.0771344)j+15}}{\bigg |}=0.1=-20dB\end{aligned}}$

Deviation from Linear Phase

Deviation from Linear Phase, $\phi _{DLP}(\omega )$, sometimes referred to as just, "phase deviation", is the difference between the phase response, $\phi (\omega )$, and the linear portion of the phase response $\phi _{L}(\omega )$, and is a useful measurement to determine the linearity of $\phi (\omega )$.

A convenient means to measure $\phi _{DLP}(\omega )$ is to take the simple linear regression of $\phi (\omega )$ sampled over a frequency range of interest, and subtract it from the actual $\phi (\omega )$. An ideal linear function would be expected to have a value of 0 across the frequency range of interest, such as the pass band of a filter. A real world measured phase function would be expected to deviate from 0 by a finite amount across the frequency range of interest.

Advantage over group delay

An advantage of measuring or calculating $\phi _{DLP}(\omega )$ over measuring or calculating group delay, $gd(\omega )$, is $\phi _{DLP}(\omega )$ always converges to 0 as the phase becomes linear, whereas $gd(\omega )$ converges on a finite quantity that may not be known ahead of time. Given this, a linear phase optimizing function may more easily be executed with a $\phi _{DLP}(\omega )=0$ goal that with a $gd(\omega )=constant$ goal when the value for $constant$ is not necessarily known.

Group delay from transfer function polynomials

If a transfer function or Sij of a scattering parameter, is in a polynomial Laplace transform form, then the mathematical definition for group delay above may be solved analytically in closed form. A polynomial transfer function $P(S)$ may be taken along the $j\omega$ axis and defined as $P(j\omega )$. $\phi (\omega )$ may be determined from $P(j\omega )$, and then the group delay may be determined by solving for $-d\phi (\omega )|/d\omega$.

to determine $\phi (\omega )$ from $P(j\omega )$, use the definition of $\phi (\omega )=tan^{-1}(P(j\omega )_{imag}/P(j\omega )_{real})$. Given that $J^{2N}$ is always real, and $J^{2N+1}$is always imaginary, $\phi (\omega )$ may be redefined as $\phi (\omega )=tan^{-1}(-jP(j\omega )_{odd}/P(j\omega )_{even})$ where even and odd refer to the polynomials that contain only the even or odd order coefficients respectively. The $-j$ in the numerator merely converts the imaginary $P(j\omega )_{odd}$ numerator to a real value, since $P(j\omega )_{odd}$ by itself is purely imaginary.

${\begin{aligned}&{\frac {dtan^{-1}(f(x))}{dx}}={\frac {df(x)/dx}{1+f(x)^{2}}}\\&f(x)={\frac {-jP(j\omega )_{odd}}{P(j\omega )_{even}}}\\&{\frac {df(x)}{dx}}={\frac {P(j\omega )_{even}{\frac {d(P(j\omega )_{odd})}{dx}}--jP(j\omega )_{odd}{\frac {d(-jP(j\omega )_{even})}{dx}}}{P(j\omega )_{even}^{2}}}\end{aligned}}$

The above expressions contain four terms to calculate:

${\begin{array}{lcl}Se=P(j\omega )_{even}&=&\sum _{k=0}^{N/2}P_{2k}(j\omega )^{2k}&=&\sum _{k=0}^{N/2}P_{2k}(-1)^{k}(\omega )^{2k}\\So=P(j\omega )_{odd}&=&-j\sum _{k=1}^{(N+1)/2}P_{2k-1}(j\omega )^{2k-1}&=&\sum _{k=1}^{(N+1)/2}P_{2k-1}(-1)^{k-1}(\omega )^{2k-1}\\De={\frac {d(P(j\omega )_{even})}{dx}}&=&-j\sum _{k=1}^{N/2}2kP_{2k}(j\omega )^{2k-1}&=&\sum _{k=1}^{N/2}2kP_{2k}(-1)^{k-1}(\omega )^{2k-1}\\Do={\frac {d(P(j\omega )_{odd})}{dx}}&=&\sum _{k=1}^{(N+1)/2}{(2k-1)}P_{2k-1}(j\omega )^{2k-2}&=&\sum _{k=1}^{(N+1)/2}{(2k-1)}P_{2k-1}(-1)^{k-1}(\omega )^{2k-2}\\\\{\frac {df(x)}{dx}}&=&{\frac {SeDo-SoDe}{Se^{2}}}\end{array}}$

The equations above may be used to determine the group delay of polynomial $P(S)$ in closed form, shown below after the equations have been reduced to a simplified form.

${\text{Group Delay}}=gd(P(j\omega ))=-{\frac {d\phi (\omega )}{d\omega }}=-{\frac {(So*De+Se*Do)}{(Se^{2}+So^{2})}}{\text{ sec}}$

Polynomial ratio

A polynomial ratio of the form $P2(S)=P_{num}(S)/P_{den}(S)$, such as that typically found in the definition of filter designs, may have the group delay determined by taking advantage of the phase relation, $\phi (P1/P2)=\phi (P1)-\phi (P2)$.

${\text{Group Delay}}=gd(P2)=gd(P2_{num})-gd(P2_{den})sec$

Simple filter example

A four pole Legendre filter transfer function used in the Legendre filter example is shown below.

$T_{4}(j\omega )={\frac {1}{2.4494897(j\omega )^{4}+3.8282201(j\omega )^{3}+4.6244874(j\omega )^{2}+3.0412127(j\omega )+1}}$

The numerator group delay by inspection is zero, so only the denominator group delay need be determined.

${\begin{aligned}&Pe_{den}=2.4494897\omega ^{4}-4.6244874\omega ^{2}+1\\&Po_{den}=-3.8282201\omega ^{3}+3.0412127\omega \\&De_{den}=4(2.4494897)\omega ^{3}-2(4.6244874)\omega \\&Do_{den}=3(-3.8282201)\omega ^{2}+3.0412127\end{aligned}}$

Evaluating at $\omega$ = 1 rad/sec:

${\begin{aligned}&Pe_{den}=-1.1749977\\&Po_{den}=-0.7870074\\&De_{den}=-0.548984\\&Do_{den}=-8.4434476\end{aligned}}$

${\begin{aligned}&{\text{Group Delay}}=gd(T_{4}(j\omega ))=-{\frac {d\phi (\omega )}{d\omega }}\\&={\bigg [}0--{\frac {((-0.7870074*-0.548984)+(-1.1749977*-8.4434476))}{((-1.1749977)^{2}+(-0.7870074)^{2})}}{\bigg ]}\\&=5.1765430{\text{ sec}}\\&{\text{at }}\omega =1{\text{ rad/sec}}\end{aligned}}$

The group delay calculation procedure and results may be confirmed to be correct by comparing them to the results derived from the digital derivative of the phase angle, $\phi (\omega )$, using a small delta $\Delta \omega$ of +/-1.e-04 rad/sec.

${\begin{aligned}&{\text{Group Delay}}=gd(T_{4}(j\omega ))=-{\frac {d\phi (\omega )}{d\omega }}\\&=-(\phi (1+1e-04)-\phi (1.-1e04))/2e-04\\&=5.1765432{\text{ sec}}\\&{\text{at }}\omega =1{\text{ rad/sec}}\end{aligned}}$

Since he group delay calculated by the digital derivative using a small delta is within 7 digits of accuracy when compared to the precise analytical calculation, the group delay calculation procedure and results are confirmed to be correct.

/////////////////////////////////////////////////////////////////////////

jacobi rotation

Eigenvalues example

Jacobian rotation can be used to extract the eigenvalues in a similar manner as the triangulation example above, but by zeroing all of the cells above the diagonal, instead of the tridiagonal, and performing the Jacobian rotation directly in the cells to be zeroed, instead of an adjacent cell.

Starting with the same $A$matrix as the tridiagonal example,

${\begin{aligned}&A={\begin{bmatrix}2&5&9&11&7\\5&3&6&-2&5\\9&6&7&3&1\\11&-2&3&1&3\\7&5&1&3&4\\\end{bmatrix}}\\&{\text{eigenvalues of }}A={\begin{bmatrix}4.1714549&5.9308002&-5.3682585&24.054762&-11.788758\end{bmatrix}}\\&|A|=37662\end{aligned}}$

The first Jacobian rotation will be on the off-diagonal cell with the with the highest absolute value, which by inspection is [1,4] with a value of 11, and the rotation cell will also be [1,4], $l=4,k=1$ in the equations above. The rotation angle is the result of a quadratic solution, but it can be seen in the equation that if the matrix is symmetric, then a real solution is assured.

${\begin{aligned}\\&11(cos^{2}(\theta )-sin^{2}(\theta ))+(2-1)cos(\theta )sin(\theta )=0\\&{\text{dividing by }}cos^{2}(\theta )\\&tan^{2}(\theta )-tan(\theta )/11-1=0\\&tan(\theta )=[1/11+{\sqrt {1/11^{2}+4}}]/2=1.0464871\\&\theta =tan^{-1}(1.0464871)=-0.80810980\\&sin(\theta )=0.72298259\\&cos(\theta )=0.69086625\\&\\&{\text{More conveniountly:}}\\&r=sqrt(1.0464871^{2}+1)=1.4474582\\&sin(\theta )=1.0464871/r=0.72298259\\&cos(\theta )=1/r=0.69086625\\&\\&S={\begin{bmatrix}&0.69086625&0&0&0.72298259&0\\&0&1&0&0&0\\&0&0&1&0&0\\&-0.72298259&0&0&0.69086625&0\\&0&0&0&0&1\\\end{bmatrix}}\\&\\&T_{1}=S^{T}AS={\begin{bmatrix}-9.5113578&4.9002964&4.0488484&0&2.6671159\\4.9002964&3&6&2.2331805&5\\4.0488484&6&7&8.5794421&1\\0&2.2331805&8.5794421&12.511358&7.1334769\\2.6671159&5&1&7.1334769&4\\\end{bmatrix}}\\&{\text{eigenvalues of }}T_{1}={\begin{bmatrix}4.1714549&5.9308002&-5.3682585&24.054762&-11.788758\end{bmatrix}}\\&|T_{1}|=37662\end{aligned}}$

The first rotation iteration, $T_{1}$, produces a matrix with cells [1,4] and [4,1] zeroed, as expected. Furthermore, the eigenvalues and determinant of $T_{1}$are identical to those of $A$ and T1 is also symmetric, confirming that the Jacobian rotation was performed correctly. The next iteration for $T_{2}$ will select cell [3,4] which contains the highest absolute value, 8.5794421, of all the cells to be zeroed..

After 25 iterations of zeroing the cell with the maximum absolute value using Jacobian rotations on the cell just below it, the maximum absolute value of all off-diagonal cells is 9.0233029E-11. Assuming this convergence criteria is acceptably low for the application it is being performed for, the similar diagonalized $T$ matrix is shown below.

${\begin{aligned}&T={\begin{bmatrix}24.054762&0&0&0&0\\0&5.9308002&0&0&0\\0&0&-11.788758&0&0\\0&0&0&4.1714549&0\\0&0&0&0&-5.3682585\\\end{bmatrix}}\\&{\text{eigenvalues of }}T={\begin{bmatrix}4.1714549&5.9308002&-5.3682585&24.054762&-11.788758\end{bmatrix}}\\&|T|=37662\end{aligned}}$

The eigenvalues are now displayed across the diagonal, and may be directly extracted for use elsewhere.

Since $A$ and $T$ have identical eigenvalues and determinants and $T$ is also symmetric, $A$ and $T$ are similar matrices with $T$ being successfully diagonalized.

Tridiagonal example

Some applications may require multiple zero entries in a similarity matrix, possibly in the form of a tridiagonal matrix. Since Jacobian rotations may remove zeros from other cells that were previously zeroed, it is usually not possible to achieve tridiagonalization by simply zeroing each off-tridiagonal cell individually in a medium to large matrix. However, if Jacobian rotations are repeatedly performed on the above-tridiagonal cell with the highest absolute value using an adjacent cell just below or to the left to rotate on, then the all of the off-triangular cells are expected to converge on zero after several iterations. In the example below, $A$ is a 5X5 matrix that is to be tridiagonalized into a similar matrix, $T$.

${\begin{aligned}&A={\begin{bmatrix}2&5&9&11&7\\5&3&6&-2&5\\9&6&7&3&1\\11&-2&3&1&3\\7&5&1&3&4\\\end{bmatrix}}\\&{\text{eigenvalues of }}A={\begin{bmatrix}4.1714549&5.9308002&-5.3682585&24.054762&-11.788758\end{bmatrix}}\\&|A|=37662\end{aligned}}$

To tridiagonalize matrix $A$ into matrix $T$, the off-tridiagonal cells [1,3], [1,4], [1,5], [2,4], [2,5], and [3,5], must continue to be iteratively zeroed until the maximum absolute value of those cells is below an acceptable convergence threshold. This example will use 1.e-14.. The cells below the diagonal will be zeroed automatically, due to the symmetric nature of the matrix. The first Jacobian rotation will be on the off-tridiagonal cell with the with the highest absolute value, which by inspection is [1,4] with a value of 11. To make this entry zero, the condition specified in the above equations must be met for the cell coordinates to be zeroed ($h=1,l=4$) and for the selected rotational coordinates of $S$ ($h=1,k=3$), and are reproduced below for the fist iteration.

${\begin{aligned}\\&9sin(\theta )+11cos(\theta )=0\\&\theta =tan^{-1}(-11/9)=-0.8850668\\&sin(\theta )=-0.77395730\\&cos(\theta )=0.66323890\\&\\&{\text{More conveniountly:}}\\&r=sqrt(11^{2}+9^{2})=14.212670\\&sin(\theta )=-11/r=-0.77395730\\&cos(\theta )=9/r=0.66323890\\&\\&S={\begin{bmatrix}&1&0&0&0&0\\&0&0.66323890&0&-0.77395730&0\\&0&0&1&0&0\\&0&0.77395730&0&0.66323890&0\\&0&0&0&0&1\\\end{bmatrix}}\\&\\&T_{1}=S^{T}AS={\begin{bmatrix}2&12.083046&9&0&7\\12.083046&-0.16438356&5.2139171&0.56164384&4.8001142\\9&5.2139171&7&-4.22079&1\\0&0.56164384&-4.22079&4.1643836&-3.3104236\\7&4.8001142&1&-3.3104236&4\\\end{bmatrix}}\\&{\text{eigenvalues of }}T_{1}={\begin{bmatrix}4.1714549&5.9308002&-5.3682585&24.054762&-11.788758\end{bmatrix}}\\&|T_{1}|=37662\end{aligned}}$

The first rotation iteration, $T_{1}$, produces a matrix with cells [1,4] and [4,1] zeroed, as expected. Furthermore, the eigenvalues and determinant of $T_{1}$are identical to those of $A$ and T1 is also symmetric, confirming that the Jacobian rotation was performed correctly. The next iteration for $T_{2}$ will select cell [2,5] which contains the highest absolute value, 4.8001142, of all the cells to be zeroed..

After 10 iterations of zeroing the cell with the maximum absolute value using Jacobian rotations on the cell just below it, the maximum absolute value of all off-tridiagonal cells is 2.6e-15. Assuming this convergence criteria is acceptably low for the application it is being performed for, the similar triangularized $T$ matrix is shown below.

${\begin{aligned}&T={\begin{bmatrix}2&16.613248&0&0&0\\16.613248&10.184783&5.1109346&0&0\\0&5.1109346&4.0304188&4.5541372&0\\0&0&4.5541372&-3.3901672&0.43515335\\0&0&0&0.43515335&4.1749658\\\end{bmatrix}}\\&{\text{eigenvalues of }}T={\begin{bmatrix}4.1714549&5.9308002&-5.3682585&24.054762&-11.788758\end{bmatrix}}\\&|T|=37662\end{aligned}}$

Since $A$ and $T$ have identical eigenvalues and determinants and $T$ is also symmetric, $A$ and $T$ are similar matrices with $T$ being tridiagonalized.

////////////////////////////////////////////////////////////////////////////////////////

Matrix Similarity

///////////////////////////////////////////////////////////////////////////////////////////

Approximating lumped elements

At higher frequencies, the reactive parasitic effects of real world lumped elements, including inductors and capacitors, limits their usefulness. Therefore, it is sometimes useful to approximate the electrical characteristics of inductors and capacitors with transmission lines at the higher frequencies using Richards' Transformations and then substitute the transmission lines for the lumped elements.

///////////////////////////////////////////////////////////////////////////////////// matrix simulATION

Simulation from admittance matrix

A common method of simulating linear circuits systems is with admittance matrices, or Y matrices. The technique involves modeling the individual linear components as an N port admittance matrix, inserting the component Y matrix into a circuits nodal admittance matrix, installing port terminations at nodes that contain ports, eliminating ports without nodes though Kron reduction, converting the final Y matrix to an S or Z matrix as needed, and extracting desired measurements from the Y, Z, and/or S matrix.

Simple Chebyshev filter example

A fifth order, 50 ohm, Chebyshev filter with 1dB of pass band ripple and cutoff frequency of 1GHz designed using the Chebyshev Cauar topology and subsequent impedance and frequency scaling produces the elements shown in the table and Micro-cap schematic below.

Chebyshev filter in Micro-cap schematic

Table of Chebyshev elements to simulate

element	g-value	Type	scaled for 50 ohms and 1GHz	nodes
P1	1	port	50	1
L1	2.1348815	inductor	1.6988847E-08	1, 2
C1	1.0911073	capacitor	3.4731024E-12	2, 0
L2	3.0009229	inductor	2.3880586E-08	2, 3
C2	1.0911073	capacitor	3.4731024E-12	3, 0
L3	2.1348815	inductor	1.6988847E-08	3, 4
P2	1	port	50	4

Modeling the 2 port Y parameters

The table above provides a list of ideal elements to model along with a node attachments to simulate. Next, each non-port element must be converted into a 2X2 Y parameter model for each frequency to be simulated. For this example, a frequency of 1GHz is selected.

Elements connected to node 0, the ground node, do not need their respective Y12 or Y21 calculated, and are shown as "n/a" in the table.

Table of Chebyshev element Y parameters at 1GHz to simulate

element	admittance at 1GHz	Y11, Y22 at 1GHz	Y12, Y21 at 1GHz	nodes
P1	n/a	n/a	n/a	1
L1	-J0.0093682013	-J0.0093682013	J0.0093682013	1, 2
C1	j0.021822146	j0.021822146	n/a	2, 0
L2	-J0.0066646164	-J0.0066646164	J0.0066646164	2, 3
C2	j0.021822146	j0.021822146	n/a	3, 0
L3	-J0.0093682013	-J0.0093682013	J0.0093682013	3, 4
P2	n/a	n/a	n/a	4

Inserting the 2 port Y parameters into the nodal admittance matrix

It should be remembered that while Ideal inductor and capacitor modals consist of very simple 2x2 models where Y11 = Y22 = -Y12 = -Y21, most real world elements cannot be modeled so simply. With transmission lines and real world inductor and capacitor models, for example, Y11 != -Y12, and for some more complex passive asymmetric elements Y11 != Y22. For many active linear devices, such as operational amplifiers, Y12 != Y21. Therefore, the example in this section uses independent Y11, Y12, Y21, and Y22 to illustrate the simulation processes that applies to more complex real world devices.

Each element Y parameter is inserted into the nodal admittance matrix by summing in them into the nodes they are attached to following the rules below.

• Y11 is summed into the n x n node in the diagonal, where n is the node that the first pin, pin 1, is attached to.

If the second node is not 0, that is, not a ground:

• Y22 is summed into the m x m node in the diagonal, where m is the node that the second pin, pin 2, is attached to.
• Y12 is summed into the n x m node location
• Y21 is summed into the m x n node location

The table below shows the Chebyshev element 2x2 Y parameters summed in at the appropriate locations.

Table of Y parameter entries

node	1	2	3	4
1	L1_Y11	L1_Y12
2	L1_Y21	L1_Y22+C1_Y11+L2_Y11	L2_Y12
3		L2_Y21	L2_Y22+C2_Y11+L3_Y11	L3_Y12
5			L3_Y21	L3_Y22

Nodal admittance matrix numerical entries

To simulate the filter at 1GHz, or any frequency, the element Y parameters must be converted to numerical entries using Y parameter models appropriate for the element installed. For ideal inductors and capacitors, the well known Y11 = Y22 = -Y12 = -Y21 = $j2\pi fL$ for inductors and Y11 = Y22 = -Y12 = -Y21 =$-j/(2\pi fC)$ for capacitors are sufficient. The numerical conversion are shown in the table below.

Table of numerical Y parameters at 1GHz

node	1	2	3	4
1	-j0.0093682	0.0093682
2	0.0093682	j0.00578933	j0.00666462
3		j0.00666462	j0.00578933	0.0093682
4			0.0093682	-j0.0093682

Removing internal nodes

Since ports are only attached to node 1 and node 4, nodes 2 and 3 need to be removed through Kron reduction. The table below shows the reduced Y parameter matrix of the Chebyshev filter example simulation after nodes 2 and 4 are eliminated. The nodes of the reduced table are renumbered to 1 and 2.

Table of Kron Reduced numerical Y parameters at 1GHz

node	1	2
1	j0.0372422	-j0.0536574
2	-j0.0536574	j0.0372422

Converting to an S parameter matrix

Since the Chebyshev frequency response is observed from the S parameter matrix, namely |S12|, the next step is to convert the Y parameter matrix to an S parameter matrix, using well known Y matrix to S matrix conversions with the port impedance as the characteristic impedance (or characteristic admittance) for each node.

Simulated S parameters also allow for useful post simulation processing for things such as group delay and phase delay.

Table of S parameters with 50 ohm terminations at 1GHz

node	1	2
1	-0.356328 + j0.280539	0.551322 + j0.700266
2	0.551322 + j0.700266	-0.356328 + j0.280539

S parameter magnitudes

Since the Chebyshev frequency response is expected to be observable in |S12| as a 1dB equi-ripple response from 0 to 1GHz, the complex S parameter entries need to be converted to their respective magnitudes, using the standard $|S_{ij}|={\sqrt {S_{ij{\text{ real}}}^{2}+S_{ij{\text{ imag}}}^{2}}}$.

Table of |S_ij| parameters with 50 ohm terminations at 1GHz

node	1	2
1	0.45351050	0.89125104
2	0.89125104	0.45351050

Check the results

It may be useful to do some quick validity checks at this point. Since the example Chebyshev filter design requirement is for -1dB attenuation at the cutoff frequency of 1GHz, |S12| at 1 GHz is expected to be -1dB. Furthermore, since all simulation elements are ideal lumped elements, the well known relation, |S₁₁|²+|S₁₂|² = 1 applies at all frequencies, including 1GHz.

Simulation validity Tests at 1GHz

	required condition	actual results	Status
1	20log10(|S12|) = -1dB	20log10(0.89125104) = -1dB	Valid
2	|S12|2+|S12|2 = 1	0.453510502+0.891251042 = 1	Valid

Full frequency Simulation

Chebyshev filter example simulation

The final validity test for the example is to simulate the Chebyshev filter frequency response through the full useful range, which will be taken to be 100 MHz to 5 GHz for this case. This range should permit viewing of the equi-ripple |S12| of the pass band between 0 and -1 dB, somewhat steep stop band |S12| falling off at 1GHz, and an equi-ripple |S12| at the expected peak values of 20log10(.4535...) = -6.86825 dB.

Since all simulation outputs conform to the expected results, the Chebyshev filter example simulation is confirmed to be correct.

Matrix parameters

The simulation of transmission lines embedded into larger systems generally utilize admittance parameters (Y matrix), impedance parameters (Z matrix), and/or scattering parameters (S matrix) that embodies the full transmission line model needed to support the simulation.

Admittance parameters

Admittance (Y) parameters may be defined by applying a fixed voltage to one port (V1) of a transmission line with the other end shorted to ground and measuring the resulting current running into each port (I1, I2) and computing the admittance on each port as a ratio of I/V The admittance parameter Y11 is I1/V1, and the admittance parameter Y12 is I2/V1. Since transmission lines are electrically passive and symmetric devices, Y12 = Y21, and Y11 = Y22.

For lossless and lossy transmission lines respectively, the Y parameter matrix is as follows:

$Y_{\text{Lossless}}={\begin{bmatrix}{\frac {-jcot(j\beta l)}{Z_{o}}}&{\frac {jcsc(j\beta l)}{Z_{o}}}\\{\frac {jcsc(j\beta l)}{Z_{o}}}&{\frac {-jcot(j\beta l)}{Z_{o}}}\end{bmatrix}}{\text{ }}Y_{\text{Lossy}}={\begin{bmatrix}{\frac {coth(\gamma l)}{Z_{o}}}&{\frac {-csch(\gamma l)}{Z_{o}}}\\{\frac {-csch(\gamma l)}{Z_{o}}}&{\frac {coth(\gamma l)}{Z_{o}}}\end{bmatrix}}$

Impedance parameters

Impedance (Z) parameter may defines by applying a fixed current into one port (I1) of a transmission line with the other port open and measuring the resulting voltage on each port (V1, V2) and computing the impedance parameter Z11 is V1/I1, and the impedance parameter Z12 is V2/I1. Since transmission lines are electrically passive and symmetric devices, V12 = V21, and V11 = V22.

In the Y and Z matrix definitions, $Y=Z^{-1}$ and $Z=Y^{-1}$. Unlike ideal lumped 2 port elements (resistors, capacitors, inductors, etc.) which do not have defined Z parameters, transmission lines have an internal path to ground, which permits the definition of Z parameters.

For lossless and lossy transmission lines respectively, the Z parameter matrix is as follows:

$Z_{\text{Lossless}}={\begin{bmatrix}-jZ_{o}cot(\beta l)&-jZ_{o}csc(\beta l)\\-jZ_{o}csc(\beta l)&-jZ_{o}cot(\beta l)\end{bmatrix}}{\text{ }}Z_{\text{Lossy}}={\begin{bmatrix}Z_{o}coth(\gamma l)&Z_{o}csch(\gamma l)\\Z_{o}csch(\gamma l)&Z_{o}coth(\gamma l)\end{bmatrix}}$

Scattering parameters

Scattering (S) matrix parameters model the electrical behavior of the transmission line with matched loads at each termination.

For lossless and lossy transmission lines respectively, the S parameter matrix is as follows, using standard hyperbolic to circular complex translations.

$S_{\text{Lossless}}={\begin{bmatrix}{\frac {(Z_{o}^{2}-Z_{p}^{2})sin(\beta l)}{(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)-j2Z_{o}Z_{p}cos(\beta l)}}&{\frac {2Z_{o}Z_{p}}{j(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)+2Z_{o}Z_{p}cos(\beta l)}}\\{\frac {2Z_{o}Z_{p}}{j(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)+2Z_{o}Z_{p}cos(\beta l)}}&{\frac {(Z_{o}^{2}-Z_{p}^{2})sin(\beta l)}{(Z_{o}^{2}+Z_{p}^{2})sin(\beta l)-j2Z_{o}Z_{p}cos(\beta l)}}\end{bmatrix}}{\text{ }}S_{\text{Lossy}}={\begin{bmatrix}{\frac {(Z_{o}^{2}-Z_{p}^{2})sinh(\gamma l)}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}&{\frac {2Z_{o}Z_{p}}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}\\{\frac {2Z_{o}Z_{p}}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}&{\frac {(Z_{o}^{2}-Z_{p}^{2})sinh(\gamma l)}{(Z_{o}^{2}+Z_{p}^{2})sinh(\gamma l)+2Z_{o}Z_{p}cosh(\gamma l)}}\end{bmatrix}}$

Variable definitions

In all matrix parameters above, the following variable definitions apply:

$Z_{o}$ = characteristic impedance

Zp = port impedance, or termination impedance

$\gamma =\alpha +j\beta$ = the propagation constant per unit length

$\alpha$ = attenuation constant in nepers per unit length

$\beta ={\frac {2\pi }{\lambda }}={\frac {\omega }{V}}$ = wave number or phase constant radians per unit length

$\omega$ = frequency radians / second

$V={\frac {1}{\sqrt {LC}}}={\frac {V_{C}}{\sqrt {E_{re}}}}$ = Speed of propagation

$\lambda$ = wave length in unit length

L = inductance per unit length

C = capacitance per unit length

$E_{re}$ = effective dielectric constant

$V_{C}$ = 299,792,458 meters / second = Speed of light in a vacuum

//////////////////////////////////////////////////////////////////////////////////////////////

Synthesizing Gaussian filter polynomials

The Gaussian transfer function polynomials may be synthesized using a Taylor series expansion of the square of Gaussian function of the form $\epsilon ^{-a\omega ^{2}}$ where $a$ is set such that $\epsilon ^{-a\omega ^{2}}={\sqrt {1/2}}$ (equivalent of -3.01dB) at $\omega =1$. The value of $a$ may be calculated with this constraint to be $a=-log{\bigg (}{\sqrt {1/2}}{\bigg )}$, or 0.34657359 for an approximate -3.010 dB cutoff attenuation. If an attenuation of other than -3.010 dB is desired,$a$ may be recalculated using a different attenuation, $a=log(10^{(|dB|/20)})$.

To meet all above criteria, $F(\omega )$ must be of the form obtained below, with no stop band zeros,

$F(\omega )=\epsilon ^{-a\omega ^{2}}{\sqrt {(\epsilon ^{-a\omega ^{2}})^{2}}}={\sqrt {\frac {1}{\epsilon ^{2a\omega ^{2}}}}}$

To complete the transfer function, $\epsilon ^{2a\omega ^{2}}$may be approximated with a Taylor series expansion about 0. The full Taylor series for $\epsilon ^{2a\omega ^{2}}$ is shown below..

$\epsilon ^{2a\omega ^{2}}=\sum _{k=0}^{\infty }{\frac {(2a)^{k}\omega ^{2k}}{k!}}$

The ability of the filter to simulate a true Gaussian function depends on how many terms are taken from the series. The number of terms taken beyond 0 establishes the order N of the filter.

$F_{N}(\omega )={\sqrt {\frac {1}{\sum _{k=0}^{\mathbb {N} }{\frac {(2a)^{k}\omega ^{2k}}{k!}}}}}$

For the frequency axis, $\omega$ is replace with $j\omega$.

$F_{N}(j\omega )={\sqrt {\frac {1}{\sum _{k=0}^{\mathbb {N} }{\frac {(2a)^{k}(j\omega )^{2k}}{k!}}}}}{\bigg |}_{\text{left half plane}}$

Since only only half the poles are located in the left half plane, selecting only those poles to build the transfer function also serves to square root the equation, as is seen above.

Simple 3rd order example

A 3rd order Gaussian filter with a -3.010 dB cutoff attenuation at $\omega$ = 1 requires the use of terms k=0 to k=3 in the Taylor series to produce the squared Gaussian function.

$F_{3}((j\omega )^{2})={\frac {1}{1.33333a^{3}(j\omega )^{6}+2a^{2}(j\omega ^{4})+2a(j\omega )^{2}+1}}={\frac {1}{-1.33333a^{3}\omega ^{6}+2a^{2}\omega ^{4}-2a\omega ^{2}+1}}$

Absorbing $a$ into the coefficients, factoring using a root finding algorithm, and building the polynomials using only the left half plane poles yields the transfer function for a third order Gaussian filter with the required -3.010 dB cutoff attenuation.

$F_{3}(j\omega )={\frac {1}{0.2355931(j\omega )^{3}+1.0078328(j\omega )^{2}+1.6458471(j\omega )+1}}$

A quick sanity check of evaluating $F_{3}(j)$ yields a magnitude of -2.986 dB, which represents an error of only ~0.8% from the desired -3.010 dB. This error will decrease as the number of orders increases. In addition, the error at higher frequencies will be more pronounced for all Gaussian filters, bug will also decrease as the order of the filter increases.

/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Synthesizing the characteristic polynomials

The solution to N order Optimum L filter characteristic polynomial synthesis emanates from solving for the characteristic polynomial, $L_{N}(\omega ^{2})$, given the below constraints and definitions.

${\begin{aligned}&L_{N}(0)=0\\&L(1)=1\\&{dL_{N}(\omega ^{2}) \over d\omega }\geq {\text{ 0 for 0 }}\leq \omega \leq 1\\&{dL_{N}(\omega ^{2}) \over d\omega }{\biggr |}_{\omega =1}{\text{ is maximum}}\\\end{aligned}}$

The odd order case and even order case may both be solved using Legendre polynomials as follows.

${\begin{aligned}&{\text{N Odd:}}\\&L_{N}(\omega ^{2})={\frac {2}{N+1}}\int _{-1}^{2\omega ^{2}-1}{\bigg (}\sum _{i=0}^{i=k}a_{i}P_{i}(x){\bigg )}^{2}dx\\&{\text{Where}}\\&P_{i}(x){\text{ is the Legendre polynomial of the first kind of order i}}\\&k={\frac {N-1}{2}}\\&a_{i}={\frac {2i+1}{\sqrt {2(k+1)}}}\\&\\&\\&{\text{N Even:}}\\&L_{N}(\omega ^{2})=\int _{-1}^{2\omega ^{2}-1}(x+1){\bigg (}\sum _{i=0}^{i=k}a_{i}P_{i}(x){\bigg )}^{2}dx\\&{\text{Where}}\\&k={\frac {N-2}{2}}\\&a_{i}={\begin{cases}{\frac {2i+1}{\sqrt {(k+2)(k+1)}}},&{\text{if }}i{\text{ is odd and }}k{\text{ is odd OR }}i{\text{ is even and }}k{\text{ is even}}\\0,&{\text{otherwise}}\\\end{cases}}\\\end{aligned}}$

Frequency response and transfer function

The magnitude frequency magnitude is created using the following formula. Since the Optimum "L" characteristic function is already in squared form, it should not be squared again as is done for other filter types such as Chebyshev filters and Butterworth filters.

${\begin{aligned}&T(\omega )={\sqrt {\frac {1}{1+\epsilon ^{2}L_{N}(\omega ^{2})}}}\\&\epsilon ^{2}=10^{|\delta |/10}-1.\\&\delta ={\text{magnitude attenuation of the passband in dB, usually 3.0103}}\\\end{aligned}}$

To obtain the transfer function, $T(j\omega )$, make the $L_{N}(\omega ^{2})$ coefficients all positive to account the $j\omega$ frequency axis, and then use the left half plane poles to construct $T(j\omega )$.

${\begin{aligned}&T(j\omega )={\sqrt {\frac {1}{a+\epsilon ^{2}L_{N}((j\omega )^{2})}}}{\bigg |}_{\text{Left half plane}}\\&{\text{Where:}}\\&a={\begin{cases}1,&{\text{if }}N{\text{ is even}}\\-1,&{\text{if }}N{\text{ is odd}}\end{cases}}\\&\epsilon ^{2}=10^{|\delta |/10}-1.\\&\delta ={\text{magnitude attenuation of the passband in dB, usually 3.010}}\\\end{aligned}}$

The, "Left Half Plane" constraint refers to finding the roots in all the polynomials contained in the brackets, selecting only roots in the left half plane, and recreating the polynomials from those roots.

Example: 4th order transfer function

N = 4 (forth order), pass band attenuation = -3.010 at 1 r/s.

A forth order filter has a value for k of 1, which is odd, so the summation uses only odd values of i for $a_{i}$and $P_{i}(x)$, which includes only the i=1 term in the summation.

The transfer function, $T_{4}(j\omega )$, may be derived as follows:

${\begin{aligned}&k={\frac {N-2}{2}}=1{\text{ (}}k{\text{ is odd)}}\\&a_{1}={\frac {2(1)+1}{\sqrt {((1)+2)((1)+1)}}}=1.2247449\\&P_{1}(x)=x\\&(x+1){\bigg (}\sum _{i=0}^{i=k}a_{i}P_{i}(x){\bigg )}^{2}=(x+1){\bigr (}1.2247449(x){\bigr )}^{2}=1.5x^{3}+1.5x^{2}\\&L_{4}(x^{2})=\int _{-1}^{2x^{2}-1}1.5x^{3}+1.5x^{2}{\text{ }}dx=6x^{8}-8x^{6}+3x^{4}\\&L_{4}(x^{2})=6x^{8}-8x^{6}+3x^{4}\\&L_{4}(j\omega ^{2})=6(j\omega )^{8}+8(j\omega )^{6}+3(j\omega )^{4}\\&echo={\sqrt {\epsilon ^{3.0103/10}-1}}=1\\&T_{4}(j\omega )={\bigg [}{\frac {1}{1+1^{2}(6(j\omega )^{8}+8(j\omega )^{6}+3(j\omega )^{4})}}{\bigg ]}_{\text{Left Half Plane}}\\&\\&T_{4}(j\omega )={\frac {1}{2.4494897(j\omega )^{4}+3.8282201(j\omega )^{3}+4.6244874(j\omega )^{2}+3.0412127(j\omega )+1}}\end{aligned}}$

A quick sanity check of $T_{4}(j)$ computes a value of -3.0103dB, which is what is expected.

Table of first 10 characteristic polynomials

N $L_{N}(\omega ^{2})$ 1 ${\textstyle \omega ^{2}}$ 2 ${\textstyle \omega ^{4}}$ 3 ${\textstyle 3\omega ^{6}-3\omega ^{4}+\omega ^{2}}$ 4 ${\textstyle 6\omega ^{8}-8\omega ^{6}+3\omega ^{4}}$ 5 ${\textstyle 20\omega ^{10}-40\omega ^{8}+28\omega ^{6}-8\omega ^{4}+\omega ^{2}}$ 6 ${\textstyle 50\omega ^{12}-120\omega ^{10}+105\omega ^{8}-40\omega ^{6}+6\omega ^{4}}$ 7 ${\textstyle 175\omega ^{14}-525\omega ^{12}+615\omega ^{10}-355\omega ^{8}+105\omega ^{6}-15\omega ^{4}+\omega ^{2}}$ 8 ${\textstyle 490\omega ^{16}-1668\omega ^{14}+2310\omega ^{12}-1624\omega ^{10}+615\omega ^{8}-120\omega ^{6}+10\omega ^{4}}$ 9 ${\textstyle 1764\omega ^{18}-7056\omega ^{16}+11704\omega ^{14}-10416\omega ^{12}+5376\omega ^{10}-1624\omega ^{8}+276\omega ^{6}-24\omega ^{4}+\omega ^{2}}$ 10 ${\textstyle 5292\omega ^{20}-23520\omega ^{18}+44100\omega ^{16}-45360\omega ^{14}+27860\omega ^{12}-10416\omega ^{10}+2310\omega ^{8}-280\omega ^{6}+15\omega ^{4}}$

The table is calculated from the above equations for $L_{N}(\omega ^{2})$

/////////////////////////////////////////////////////////////////

Even order modified Chebyshev polynomials

Some applications rely on Chebyshev polynomials but may be unable to accommodate the lack of a root at zero, which rules out the use of standard Chebyshev polynomials for these kinds of applications. Even order Chebyshev filter designs using equally terminated passive networks are an example of this. However, even order Chebyshev polynomials may be modified to move the lowest roots down to zero while still maintaining the desirable Chebyshev equi-ripple effect. Such modified polynomials contain two roots at zero, and may be referred to as even order modified Chebyshev polynomials. Even order modified Chebyshev polynomials may be created from the Chebyshev nodes in the same manner as standard Chebyshev polynomials.

${\begin{aligned}&P_{N}=\prod _{i=1}^{N}(x-C_{i})\\&{\text{Where }}\\&P_{N}{\text{ is an N order Chebyshev polynomial}}\\&C_{i}{\text{ is the ith Chebyshev node}}\end{aligned}}$

In the case of even order modified Chebyshev polynomials, the even order modified Chebyshev nodes are used to construct the even order modified Chebyshev polynomials.

${\begin{aligned}&Pe_{N}=\prod _{i=1}^{N}(x-Ce_{i})\\&{\text{Where }}\\&Pe_{N}{\text{ is an N order even order modified Chebyshev polynomial}}\\&Ce_{i}{\text{ is the ith even order modified Chebyshev node}}\end{aligned}}$

For example, the 4th order Chebyshev polynomial from the example above is $X^{4}-X^{2}+.125$, which by inspection contains no roots of zero. Creating the polynomial from the the even order modified Chebyshev nodes creates a 4th order even order modified Chebyshev polynomial of $X^{4}-.828427X^{2}$, which by inspection contains two roots at zero, and may be used in applications requiring roots at zero.

//////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Chebyshev Nodes

Even order modified Chebyshev nodes

Many applications for Chebyshev nodes, such as the design of equally terminated passive Chebyshev filters, cannot use use Chebyshev nodes directly, due to the lack of a root at 0. However, the Chebyshev nodes may be modified into a usable form by translating the roots down such that the lowest roots are moved to zero, thereby creating two roots at zero of the modified Chebyshev nodes.

The even order modification translation is:

$X_{k}Even={\sqrt {\frac {X_{k}^{2}-X_{n/2}^{2}}{1-X_{n/2}^{2}}}}{\text{ For }}n>2$

The sign of the ${\sqrt {}}$ function is chosen to be the same as the sign of $X_{k}$.

For example, the Chebyshev nodes for a 4th order Chebyshev function are, {0.92388,0.382683,-0.382683,-0.92388}, and $X_{n/2}^{2}$ is $0.382683^{2}$, or 0.146446. Running all the nodes through the translation yields $X_{k}Even$ to be {0.910180, 0, 0, -0.910180}.

The modified even order Chebyshev nodes now contains two nodes of zero, and is suitable for use in designing even order Chebyshev filters with equally terminated passive element networks.

/////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Chebyshev II

Even order modifications

Just like Chebyshev filter even order filters, the standard Chebyshev II even order filter cannot be implemented with equally terminated passive elements. In the Chebyshev Ii case, this is due to finite attenuation of S12 in the stop band. However, even order Chebyshev II filters may be modified by translating the highest frequency finite transmission zero to infinity, while maintaining the equi-ripple functions of the Chebyshev II stop band. To do this translation, simply use an even order modified Chebyshev function to place the Chebyshev II poles and zeros to create the Chebyshev II transfer function.

Setting the cutoff attenuation

The standard cutoff attenuation as described is the same at the pass band ripple attenuation. However, just as in Chebyshev filters, it is useful to set the cutoff attenuation to a desired value, and for the same reasons. Setting the Chebyshev II cutoff attenuation is the same as for Chebyshev, except the arithmetic attenuation and ripple entries are inverted in the equation and the poles and zeros are multiplied by the result, as opposed to divided by in the Chebyshev case..

${\begin{aligned}p_{A}&=p_{1}*T_{n}^{-1}{\Biggr (}{\sqrt {\frac {10^{{-\delta }/10}-1}{10^{-\alpha /10}-1}}},n{\Biggr )}\qquad &{\text{For }}0>\delta >-\infty {\text{ and }}0>\alpha \geq \delta \\&=p_{1}*cosh{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{-\delta /10}-1}{10^{-\alpha /10}-1}}}{\Bigr )}{\Biggr )}&{\text{For }}0>\delta >-\infty {\text{ and }}0>\alpha \geq \delta \\\end{aligned}}$

Even order modified cutoff attenuation adjustment

The same even order adjustment to the poles and zeros that was used for the Chebyshev case may also be used for the Chebyshev II case, except the poles are multiplied by the result.

${\begin{aligned}p_{A}=p_{1}{\sqrt {\frac {cosh^{2}{\Biggr (}{\frac {1}{n}}cosh^{-1}{\Bigr (}{\sqrt {\frac {10^{-\delta /10}-1}{10^{-\alpha /10}-1}}}{\Bigr )}{\Biggr )}-cos^{2}({\frac {\pi (n-1)}{2n}})}{1-{cos^{2}({\frac {\pi (n-1)}{2n}})}}}}{\text{ For }}0>\delta >-\infty {\text{ and }}\delta \geq \alpha >-\infty \\\end{aligned}}$

//////////////////////////////////////////////////////////////////////////////////////////////////////////

Newton's method for systems of nonlinear equations

When multiple nonlinear equations need to be solved for more than one variable, Newton's Method for Systems of Equations may be used to solve the equations simultaneously for the solution vector. The process is very similar to solving Newton's method for one variable, except the single nonlinear equation is replaced with a system of nonlinear equations, the derivative is replaced with a Jacobian matrix of partial derivatives, and the subtraction is replaced with a vector subtraction. Newton's method for systems of nonlinear equations reduces to Newton's method for nonlinear equations when the system of equations includes only one equation.

Procedure

For single equations, Newton's method consists of the following iterations until the iterations no longer produce any changes to $x$ of significance,

$x_{k+1}=x_{k}-{\frac {f(x_{k})-y_{k}}{f'(x_{k})}}$

For systems of equations, the same is true, but for vector $X$ instead of scalar $x$,

${\begin{aligned}&X_{k+1}=X_{k}-C(X_{k})\\\end{aligned}}$

Where $C(X_{k})$ is the solution vector to $J(X_{k})C(X_{k})=(F(X_{k})-Y)$

$J(X_{k})$ is the Jacobian matrix for $X_{k}$

$Y$ is a vector of known values

If the $Y$ vector is set to all zeros, the defining equations may be rewritten in the commonly found form below.

${\begin{aligned}&X_{k+1}=X_{k}-J(X_{k})^{-1}F(X_{k})\\\end{aligned}}$

or

${\begin{aligned}&J(X_{k})(X_{k+1}-X_{k})=-F(X_{k})\\\end{aligned}}$

Simple example

For example, the following set of equations needs to be solved for vector of points $(x_{1},x_{2})$, given the vector of known values, (2,3).

${\begin{array}{lcr}5x_{1}^{2}+x_{1}x_{2}+sin^{2}(2x_{2})&=2\\e^{2x_{1}-x_{2}}+5x_{2}&=3\end{array}}$

the function vector, $F(X_{k})$, and Jacobian Matrix, $J(X_{k})$ for iteration k, and the vector of known values, $Y$, are defined below.

${\begin{aligned}&F(X_{k})={\begin{bmatrix}{\begin{aligned}&5x_{1}^{2}+x_{1}x_{2}^{2}+sin^{2}(2x_{2})\\&e^{2x_{1}-x_{2}}+4x_{2}\end{aligned}}\end{bmatrix}}_{k}\\&J(X_{k})={\begin{bmatrix}{\frac {\partial {f(x_{1})}}{\partial {x_{1}}}}&{\frac {\partial {f(x_{1})}}{\partial {x_{2}}}}\\{\frac {\partial {f(x_{2})}}{\partial {x_{1}}}}&{\frac {\partial {f(x_{2})}}{\partial {x_{2}}}}\end{bmatrix}}_{k}={\begin{bmatrix}{\begin{aligned}&10x_{1}+x_{2}^{2}&&2x_{1}x_{2}+4sin(2x_{2})cos(2x_{2})\\&2e^{2x_{1}-x_{2}}&&-e^{2x_{1}-x_{2}}+4\end{aligned}}\end{bmatrix}}_{k}\\&Y={\begin{bmatrix}2\\3\end{bmatrix}}\end{aligned}}$

Note that $F(X_{k})$ could have been rewritten to absorb $Y$, and thus eliminate $Y$ from the equations. The equation to solve for each iteration are

${\begin{aligned}{\begin{bmatrix}{\begin{aligned}&10x_{1}+x_{2}^{2}&&2x_{1}x_{2}+4sin(2x_{2})cos(2x_{2})\\&2e^{2x_{1}-x_{2}}&&-e^{2x_{1}-x_{2}}+4\end{aligned}}\end{bmatrix}}_{k}{\begin{bmatrix}c_{1}\\c_{2}\end{bmatrix}}_{k+1}={\begin{bmatrix}5x_{1}^{2}+x_{1}x_{2}^{2}+sin^{2}(2x_{2})-2\\e^{2x_{1}-x_{2}}+4x_{2}-3\end{bmatrix}}_{k}\end{aligned}}$

and

$X_{k+1}=X_{k}-C_{k+1}$

The iterations should be repeated until ${\bigg [}\sum _{i=1}^{i=2}|f(x_{i})_{k}-(y_{i})_{k}|{\bigg ]}<E$, where $E$ is a value acceptably small enough to meet application requirements.

If vector $X_{0}$ is initially chosen to be ${\begin{bmatrix}1&1\end{bmatrix}}$, that is, $x_{1}=1{\text{ and }}x_{2}=1$, and $E$ is chosen to be 1.e-03, then the example converges after four iterations to a value of $X_{4}=(0.567297,-0.309442)$.

Iterations

The following iterations were made during the course of the solution.

Iteration Convergence Sequence

Iteration	Variable	Variable Contents
0	X	${\begin{bmatrix}1&1\end{bmatrix}}$
	F(X)	${\begin{bmatrix}6.82682&6.71828\end{bmatrix}}$
1	J	${\begin{bmatrix}11&0.486395\\5.43656&1.28172\end{bmatrix}}$
	C	${\begin{bmatrix}0.382211&1.27982\end{bmatrix}}$
	X	${\begin{bmatrix}0.617789&-0.279818\end{bmatrix}}$
	F(X)	${\begin{bmatrix}2.23852&3.43195\end{bmatrix}}$
2	J	${\begin{bmatrix}6.25618&-2.1453\\9.10244&-0.551218\end{bmatrix}}$
	C	${\begin{bmatrix}0.0494549&0.0330411\end{bmatrix}}$
	X	${\begin{bmatrix}0.568334&-0.312859\end{bmatrix}}$
	F(X)	${\begin{bmatrix}2.01366&3.00966\end{bmatrix}}$
3	J	${\begin{bmatrix}5.78122&-2.25449\\8.52219&-0.261095\end{bmatrix}}$
	C	${\begin{bmatrix}0.00102862&-0.00342339\end{bmatrix}}$
	X	${\begin{bmatrix}0.567305&-0.309435\end{bmatrix}}$
	F(X)	${\begin{bmatrix}2.00003&3.00006\end{bmatrix}}$
4	J	${\begin{bmatrix}5.7688&-2.24118\\8.47561&-0.237805\end{bmatrix}}$
	C	${\begin{bmatrix}7.73132E-06&6.93265E-06\end{bmatrix}}$
	X	${\begin{bmatrix}0.567297&-0.309442\end{bmatrix}}$
	F(X)	${\begin{bmatrix}2&3\end{bmatrix}}$

${\begin{aligned}&{\text{Iteration 0 (Starting Point)}}\\&X=(1,1)\\&F(X)={\begin{bmatrix}6.82682&6.71828\end{bmatrix}}\\\\&{\text{Iteration 1}}\\&J={\begin{bmatrix}11&0.486395\\5.43656&1.28172\end{bmatrix}}\\&C={\begin{bmatrix}0.382211&1.27982\end{bmatrix}}\\&X={\begin{bmatrix}0.617789&-0.279818\end{bmatrix}}\\&F(X)={\begin{bmatrix}2.23852&3.43195\end{bmatrix}}\\\\&{\text{Iteration 2}}\\&J={\begin{bmatrix}6.25618&-2.1453\\9.10244&-0.551218\end{bmatrix}}\\&C={\begin{bmatrix}0.0494549&0.0330411\end{bmatrix}}\\&X={\begin{bmatrix}0.568334&-0.312859\end{bmatrix}}\\&F(X)={\begin{bmatrix}2.01366&3.00966\end{bmatrix}}\\\\&{\text{Iteration 3}}\\&J={\begin{bmatrix}5.78122&-2.25449\\8.52219&-0.261095\end{bmatrix}}\\&C={\begin{bmatrix}0.00102862&-0.00342339\end{bmatrix}}\\&X={\begin{bmatrix}0.567305&-0.309435\end{bmatrix}}\\&F(X)={\begin{bmatrix}2.00003&3.00006\end{bmatrix}}\\\\&{\text{Iteration 4}}\\&J={\begin{bmatrix}5.7688&-2.24118\\8.47561&-0.237805\end{bmatrix}}\\&C={\begin{bmatrix}7.73132E-06&6.93265E-06\end{bmatrix}}\\&X={\begin{bmatrix}0.567297&-0.309442\end{bmatrix}}\\&F(X)={\begin{bmatrix}2&3\end{bmatrix}}\\\\\end{aligned}}$

Practical considerations

Newton's Method for systems of equations especially large sets of equations, can be finickier than for single equations. Care should be taken to insure a solution is found within a reasonable number of iterations.

Singular matrices

The solution to the linear set of equations that must be solved may not necessarily result in a usable non-singular solution. This can be because the set of equations has no solution, or because of a poorly chosen starting vector for $X_{0}$. For example, had the initial $X_{0}$been chosen to be (0,0), the first iteration should have resulted in a singular matrix and the convergence would have failed. Care should be taken to choose a valid starting $X_{0}$that is known to produce a non-singular first iteration.

Asymptotic divergence to infinity

Even though a system of equations is known to have a solution, the iterations may asymptotically diverge to infinity. This is especially more likely to happen with large number of equations. However, this condition can be mitigated or prevented by selecting a good starting point for $X_{0}$. In addition, the following steps may further mitigate divergence.

• Limit the range of the linear solution, the C vector, to a small range, but large enough to converge in a reasonable number of iterations.
• Limit the $X$vector iterations to known limits for each $x_{k}$ entry.
• Scale down the C vector entries slightly to slow down the convergence. Slow convergences are less likely to go divergent.

Slow convergence

In time sensitive applications, convergence speed is importance in that slow convergence can have detrimental affects on the application that is being supported. Convergence time can be minimized through the following steps.

• Good selection of the initial $X_{0}$starting point is very importance in minimizing the number of iterations required for an acceptable convergence error. For example, the example above, had the initial $X_{0}$ been chosen to be (2,2) instead of (1,1), then seven iterations would have been required instead of four.
• Limit the $X$ vector iterations to known limits for each $x_{k}$ entry. The $X$ vector does not have diverge to slow things down. If no limit has been placed on the vector, or the limit is too big, the iterations may spend too much time recomputing large values instead of converging.
• Scale down the C vector entries slightly to slow down the convergence. This may help prevent the iterations from jumping around and taking too long to converge.
• Select a conference error point as large as possible that still meets the application requirements. For example, had an error of 1.e-15 been chosen for the example above, six iterations should have been required, as opposed to only four needed to converge to an error of 1,e-03. The additional two iterations may be acceptable for high precision applications, but would be a waste for applications that only need light precision.

Insure a solution does exist

It is much easier to determine that a known solution exists or does not exist with single equations. For example, $X^{2}=4$ has an obvious known solution (2), while $X^{2}=-4$ is obvious that no solution exists in the set of real number. With sets of equations, especially large sets, it is far more difficult to determine that a solution exists or does not exist. If a solution does not exists, the iterations will certainly fail, but if a solution does exist, the iterations may still fail. Upfront work may be required to determine that a solution does or does not exist before making conclusions.

Multiple solutions

It is easier to determine that multiple solutions exist with single equations. The $X^{2}=4$ from the preceding paragraph, for example, has a solution of $X=2{\text{ and }}X=-2$. For sets of equations, especially large sets, it may not be so obvious, and even if it is obvious, it may be more difficult to insure convergence takes place at the desired solution. Care should taken to start with an $X_{0}$ as near as possible to the desired solution., and that limits are installed on the individual $X$ entries to move the iterations away from undesirable solutions and toward the desirable solutions(s). It should be noted that many solutions exist in the example used above.

Digital verses continuous derivatives

Derivatives should be calculated using continuous functions whenever possible to maximize accuracy and minimize convergence problems. If the function is unknown and not possible to calculate continuous derivatives, digital derivatives may be used, but care should be taken to maximize accuracy. Use double samples close together, if possible. If not possible, such as in a string of data, cubic interpolations are preferred due to the cubic iterations retention of a defined first derivative. If accuracy is not an issue, linear interpolations may be used, while keeping in mind that the first directives are not defined at the data point, requiring that the next or prior linear segment be used to estimate the derivative.

///////////////////////////////////////////

Bessel filters

Setting the cutoff attenuation

There is no standard set attenuation value for Bessel filters. However, −3.0103 dB is a common choice. Some applications may use a higher or lower attenuation such as −1 dB or −20 dB. Setting the cut-off attenuation frequency involves first finding the frequency that achieves the desired attenuation, which will be referred to as $\omega _{c}$, and then scaling the $H(s)$ polynomials to the inverse of that frequency. To scale the polynomials, simply append $\omega _{c}$ to the $s$ term in each coefficient, as shown in the 3 pole Bessel filter example below.

${\begin{aligned}H(s)&={\frac {15}{s^{3}+6s^{2}+15s+15}}\\H(s)'&=H(s)_{{\text{desired dB at }}\omega =1}={\frac {15}{(\omega _{c}s)^{3}+6(\omega _{c}s)^{2}+15\omega _{c}s+15}}\\\end{aligned}}$

$\omega _{c}$ may be found with Newton's method, or with root finding.

Finding attenuation frequency with Newton's method

Newton's method requires a known magnitude value and derivative magnitude value for the for $|H(j\omega _{c})|$. However, it is easier to operate on $|H(j\omega _{c})H(-j\omega _{c})|$ and use the square of the desired cutoff gain, and is just as accurate, so the square terms will be used.

To obtain $\omega _{c}$, follow the steps below.

1. If $H(s)H(-s)$ is not already available, multiply $H(s)$ by $H(-s)$ to obtain $H(s)H(-s)$.
2. negate all terms of $s^{n}$ when $(n+2)$ is divisible by $4$. That would be $s^{2}$, $s^{6}$, $s^{10}$, and so on. The modified function will be called $H_{2}(s)H_{2}(-s)$, and this modification will allow the use of real numbers instead of complex numbers when evaluating the polynomial and its derivative. the real $\omega _{a}$can now be used in place of the complex $j\omega _{a}$
3. Convert the desired attenuation in dB, $A_{dB}$, to a squared arithmetic gain value, $B_{arith}^{2}$, by using $B_{arith}^{2}=10^{A_{dB}/10}$. For example, 3.010 dB converts to 0.5, 1 dB converts to 0.79432823 and so on.
4. Calculate the modified $|H_{2}(s)H_{2}(-s)|$ in Newton's method using the real value, $\omega _{a}$. Always take the absolute value.
5. Calculate the derivative the modified $H_{2}(\omega _{a})H_{2}(-\omega _{a})$ with respect to the real value, $\omega _{a}$. DO NOT take the absolute value of the derivative.

When steps 1) through 4) are complete, the expression involving Newton's method may be written as:

$\omega _{a}=\omega _{a}-([H_{2}(\omega _{a})H_{2}(-\omega _{a})|-B^{2})/(d[H_{2}(\omega _{a})H_{2}(-\omega _{a})]/d\omega _{a})$

using a real value for $\omega _{a}$with no complex arithmetic needed. The movement of $\omega _{a}$ should be limited to prevent it from going negative early in the iterations for increased reliability. When complete, $\omega _{a}$ can used for the $\omega _{c}$ that can be used to scale the original $H(s)$ transfer function denominator. The attenuation of the modified $G(s)$ will then be virtually the exact desired value at 1 rad/sec. If performed properly, only a handful of iterations are needed to set the attenuation through a wide range of desired attenuation values for both small and very large order filters.

Finding attenuation frequency from the roots

Since $|H(j\omega _{a})|$ does not contain any phase information, directly factoring the transfer function will not produce usable results. However, the transfer function may be modified by multiplying it with $H(-s)$ to eliminate all odd powers of $H(j\omega a)$, which in turn forces $H(j\omega a)$ to be real at all frequencies, and then finding the frequency that result on the square of the desired attention.

1. If $H(s)H(-s)$ is not already available, multiply $H(s)$ by $H(-s)$ to obtain $H(s)H(-s)$.
2. Convert the desired attenuation in dB, $A_{dB}$, to a squared arithmetic gain value, $B_{arith}^{2}$, by using $B_{arith}^{2}=10^{A_{dB}/10}$. For example, 3.010 dB converts to 0.5, 1 dB converts to 0.79432823 and so on.
3. Find $P(S)=H_{num}(S)H_{num}(-S)-B_{arith}^{2}H_{den}(S)H_{den}(-S)$
4. Find the roots of P(S) using a root finding algorithm.
5. Of the set of roots from above, select the positive imaginary root for all order filters, and positive real root for even order filters.
   1. Cutoff attenuations that are above the pass band ripple or below the stop band ripple will come back with multiple roots, so the correct root will have to be selected.

Simple cut-off frequency example with root finding

A 20-dB cut-off frequency attenuation example using the 3-pole Bessel example below is set as follows.

${\begin{aligned}&H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}{\text{ (from the example below)}}\\&B_{arith}^{2}=10^{20/10}=0.01{\text{ (the arithmetic gain squared)}}\\&\\&{\text{Find }}H(s)'{\text{ such that }}|H(s)'|=-20{\text{ dB at }}\omega =1{\text{.}}\\&H(s)H(-s)={\frac {225}{-s^{6}+6s^{4}-45^{2}s+225}}\\&P(s)=225-B_{arith}^{2}(-s^{6}+6s^{4}-45^{2}s+225)=0.01s^{6}-0.06s^{4}+0.45s^{2}+222.75{\text{ (polynomial to be factored)}}\\&R=j5.0771344{\text{ (the positive imaginary root for the above polynomial)}}\\&{\text{For even order filters, use the positive real root.}}\\&\\&\omega _{-20{\text{ dB atten}}}=\omega _{c}=5.0771344{\text{ rad/sec (20 dB attenuation frequency)}}\\&H(s)'=H(s)_{A=20{\text{ dB at }}\omega =1}={\frac {15}{(5.0771344^{3})s^{3}+(6\times 5.0771344^{2})s^{2}+(15\times 5.0771344)s+15}}\\&={\frac {15}{130.87478s^{3}+154.66376s^{2}+76.157016s+15}}\\&\\&{\text{Check:}}\\&|H(j)'|={\bigg |}{\frac {15}{130.87478j^{3}+154.66376j^{2}+76.157016j+15}}{\bigg |}=0.1=-20{\text{ dB Gain}}\end{aligned}}$

////////////////////////////////////////////////////////////////////////////////////////////