Wikipedia:Reference desk/Archives/Mathematics/2007 July 16
| Mathematics desk | ||
|---|---|---|
| < July 15 | << Jun | July | Aug >> | July 17 > |
| Welcome to the Wikipedia Mathematics Reference Desk Archives |
|---|
| The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
July 16[edit]
Area under a curve[edit]
Does anyone know the formula for finding the area under a curve exactly using sumnation and limits, and w/o using integrals?
- No, because that's what an integral is. To be a little less obtuse, it heavily depends on the curve involved as to whether you can do something like this without actually invoking the Fundamental Theorem of Calculus. For a straight line, you've got no problem because it's just a trapezoid. For a parabola (and possibly other polynomial curves, I'm not sure), you can partition the horizontal axis into equally-spaced sections and take upper and lower limits and show that they converge to the same thing as the number of partitions goes to infinity. For an exponential, I'm pretty sure you can do the same (although it's rather ugly), or use a partition where the size of the intervals goes in geometric sequence. Can you provide a little more context? Confusing Manifestation 00:32, 16 July 2007 (UTC)
- My first thought was to jump to Integral#Pre-calculus_integration, which also linked to Method of exhaustion, but those seem to talk more about the history than the process. Riemann sum may be worth your while to look into. (Actually, you can probly create a limit given enough data points from Riemann sums.) --YbborTalk 00:36, 16 July 2007 (UTC)
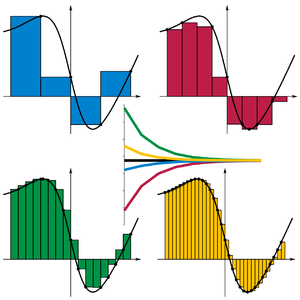
- Let's assume that the curve is given by a formula, y = f(x). Further assume that the curve is bounded in the region of interest: |f(x)| ≤ M for some constant M. For convenience, also assume that the curve "looks like a curve" — it is continuous (so that small changes in x correspond to small changes in y). Finally, assume that we have finite bounds of integration, say −∞ < a ≤ x ≤ b < ∞ Yes, we're assuming a lot; but the alternative is to get much more technical.
- Then, as Ybbor suggested, we can use Riemann sums. That is, divide the interval from a to b into n pieces (for convenience, equal width pieces). For each piece (subinterval), take a function value in that piece (for convenience, at the right end). The weighted sum of piece values times piece widths is a Riemann sum; with the convenient choices,
- As explained at integral, shrinking the largest width w (with the convenient choices, increasing n) produces a sequence of sums whose limit is the desired area. I am deliberately omitting a more complete answer, to avoid doing homework.
- Caution: This is the hard way to compute area; determining a value for these limits can be challenging. Also, the assumptions are important; without them, this method may fail. --KSmrqT 06:24, 16 July 2007 (UTC)
- Is it possible that the questioner is meaning limits in the sense of end-points, and is seeking something like Simpson's rule, which by summation gives the exact area for polynomials up to cubics?81.153.219.69 08:07, 16 July 2007 (UTC)
- Who knows...maybe? We will just have to wait for him to come back and clarify his question.--Cronholm144 08:18, 16 July 2007 (UTC)
- If that is so, the OP should definitely take a look at Gaussian quadrature. Otherwise, perhaps a concrete example can help: Suppose we want to find the are under the curve when x ranges from 0 to 1. Since this function is continuous, we may as well divide the interval to n subintervals, and evaluate the function at the right end of every subinterval. Then the area of the ith rectangle is . The total area of all rectangles is:
- And as n goes to , this goes to . -- Meni Rosenfeld (talk) 15:46, 16 July 2007 (UTC)
Structured sparsity[edit]
What does structured sparsity mean? --HappyCamper 09:25, 16 July 2007 (UTC)
- These to deal with structured sparsity as it relates to polynomial optimization, for a simpler explanation...just wait.--Cronholm144 09:39, 16 July 2007 (UTC)
Also, these might be what you are looking for.--Cronholm144 09:52, 16 July 2007 (UTC)
Fourier transform uniformly continuous?[edit]
Hi, I'm back with another question. Can anyone help me prove that the Fourier transform of an integrable function over R is uniformly continuous? I can prove that it is continuous just fine, but I'm having some issues. I need to prove that if , then the function is uniformly continuous.
I know what uniformly continuous means, so there's no problem there. I've done the basic thing, like let ε > 0 be given, assume I have some δ with |x - y| < δ, and then play with the inequality |g(x) - g(y)|, but I'm not getting anywhere. I have
- ,
but I have issues getting an |x - y| expression to show up.
I've searched around a bit, and everyone seems to cite this fact freely, but I can't find a proof for it. I imagine it's not that bad, so if anyone can point me in the right direction, I'd be grateful. Thanks! –King Bee (τ • γ) 20:59, 16 July 2007 (UTC)
- I think the estimate you have given is very bad for you. It gets rid of the oscillatory nature of the integrand which is the key here. I haven't worked out a solution, but here is a suggestion: Having chosen ε, you can now choose M as large as you please; since g is uniformly continuous on the interval , you are guaranteed the existence of a δ which works in it, so you only need to show a δ which works for . The oscillations of should be important for this task. -- Meni Rosenfeld (talk) 21:22, 16 July 2007 (UTC)
- Thanks for the quick reply. I understand your plan of attack (and am a bit embarrassed I didn't think of it myself). I also understand what you mean by "oscilliatory nature," but maybe I don't understand enough about the function to make this work. Another jab in the side, please? =) –King Bee (τ • γ) 21:37, 16 July 2007 (UTC)
- Well, you may as well treat the real and imaginary parts separately, and you may as well forget the imaginary part altogether and treat as if it was simply . When viewed as a function of t, it is oscillatory with frequency which depends on x. The integral of a function is smaller the more rapid its oscillations are, which is useful if you take x to be large. In particular, if you do integration by parts, you get a term which can help establish the necessary bounds. (Of course, the same will happen if you stick with , but keeping everything real might help somehow). -- Meni Rosenfeld (talk) 22:15, 16 July 2007 (UTC)
- Actually, I was assuming here that f is real; it doesn't really matter much, but it may be easier to prove this in the real case first, and then generalize. -- Meni Rosenfeld (talk) 22:19, 16 July 2007 (UTC)
- Addendum: The "integration by parts" part, as is, is only valid if f is differentiable. I guess something similar can be done for more general f. -- Meni Rosenfeld (talk) 12:09, 17 July 2007 (UTC)
- I have solved the problem. Your original idea coupled with the Riemann-Lebesgue lemma has done the trick! Thank you for your help.
I have another, related question however. Suppose and . I need to show that . It seems really similar to the previous question; is your advice the same, and I should keep plugging away at it, or does anyone have a different idea? –King Bee (τ • γ) 20:15, 17 July 2007 (UTC)
- Ah, yes, we have lemmas to harness the oscillations :). I think the idea is the same here, and the transformation comes to mind. -- Meni Rosenfeld (talk) 00:05, 18 July 2007 (UTC)
- Proving the Riemann-Lebesgue lemma is not hard, and I thought I could mimic the proof of that to do this one. However, my main issue lies in trying to prove that the statement is true if the function f is the characteristic function of some finite interval. Since I can't get an elementary antiderivative for , what am I to do? I don't think your transformation that you had in mind would help, unless I'm missing something painfully obvious. Ideas? –King Bee (τ • γ) 14:35, 18 July 2007 (UTC)
- Okay, I think I have the method for the solution down. Let's see what you guys think.
- First, split the integral in two:
- Let's concern ourselves with the second integral above, and use Meni's change of variable idea. Then we have
- Now, if we can show that the function is L1, we can use the Riemann-Lebesgue lemma to get that the integral above decays to 0 as u tends to . What do you think? Valid argument? –King Bee (τ • γ) 15:41, 18 July 2007 (UTC)
- Yes, I assumed it would be clear that letting will give an extra term, which is a bonus rather than a burden. As for showing that is , we can once again use ... You will then need a variant of Riemann-Lebesgue which works for a general interval (which I think is trivial but haven't thought it through). And of course, you meant "as t tends to ∞" at the end. -- Meni Rosenfeld (talk) 12:26, 19 July 2007 (UTC)
- I did, and yes, everything works out correctly. You don't really use the R-L lemma so much as you simply adapt the proof of it to this particular situation (where you're not dealing with the whole real line). Thanks for the help! I feel much better about these types of problems now. =) –King Bee (τ • γ) 14:40, 19 July 2007 (UTC)
Uncertainty in various fields[edit]
When giving error limits, there is almost always an uncertainty associated with the limits. For example, the August 2007 edition of Scientific American contains a graph on page 67 that shows various causes of radiative forcing which are thought to be driving global warming, and for each forcing an error bar is shown, which represent a 90 percent liklihood that the value lies within the error bar. Similarly, page 66 contains the statement "the updated trend over 1906 to 2005 is now 0.6 ± 0.2 degree C." There must be some unstated uncertainty associated with this tolerance; perhaps the phrase realy means there is a 90 percent probability that the trend lies between 0.4 and 0.8 degree C.
What I would like to know is whether there is/are document(s) that state what level of uncertainty is usually used in various fields when there isn't enough information to rigorously choose an uncertainty level? If this had been a biology article instead of a climate article, would the uncertainty level have been 95 percent rather than 90 percent?
I understand that on rare occasions, the economic consequences of the measurement falling outside the error bounds is known, and the budget available to deal with the outliers is known, so an appropriate error bound can be rigorously calculated, but this seldom is the case. --Gerry Ashton 22:03, 16 July 2007 (UTC)
This is not a mathematics question. May I suggest that this be moved to the Science section of the reference desk. 202.168.50.40 22:25, 16 July 2007 (UTC)
- Statistics is mathematics. I suggest this is a mathematics question, in that it asks if there is a general guide to how mathematics is applied in various fields. --Gerry Ashton 22:33, 16 July 2007 (UTC)
- It's not so much statistics as how it's applied. Not everything with mathematical content is mathematics strictly speaking. There's a somewhat better chance of getting an answer as to whether .9 is standard in climate science in the science desk. It is likely to be a .9 probability for the statement on p. 66 if .9 is used earlier in the article. Donald Hosek 23:51, 16 July 2007 (UTC)










![{\displaystyle [-M-1,M+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9d32b193abdceb96c951a42acefba0a5e1623d4)













