User:Jean Raimbault/sandbox/Random walk
One-dimensional random walk[edit]
Informal discussion[edit]
Maybe the most simple example of a random walk is the random walk on the integer number line which starts at 0 and at each step moves +1 or −1 with equal probability. This walk can be illustrated as follows. A marker is placed at zero on the number line and a fair coin is flipped. If it lands on heads, the marker is moved one unit to the right. If it lands on tails, the marker is moved one unit to the left. After the first step the counter is at 1 or -1 both with probability 0.5; after the second it can be at 0 if the flips' result was head/tails or tails/head so with probability 0.5, since that makes two outcomes out of four, or at 2 (two heads) or -2 (two tails), both with probability 0.25. See the figure below for an illustration of the possible outcomes up to 5 flips.

The walk can also be represented by the graph of its position with respect to time, as in the following figure.

Definition[edit]
To define this walk formally, take independent random variables , where each variable is either 1 or −1, with a 50% probability for either value, and set
- for .
The sequence of random variables is called the simple random walk on ; the random variable is the th-position of the walk.
Asymptotic size[edit]
The expectation of is zero. That is, the mean of all coin flips approaches zero as the number of flips increases. This follows by the finite additivity property of expectation:
The next question is: how large is the typical state at time ? A rough answer is given by the expected values of the random variables and . A calculation similar to the one above, using the independence of the random variables and the fact that , shows that:
This implies, using the Cauchy-Schwarz inequality, that , the expected translation distance after n steps, is at most of the order of . In fact, it follows from the central limit theorem that:
The law of the iterated logarithm describes the amplitude of the ocillations of the random walk: it states that for any , for almost all paths and for infinitely many .
Local central limit theorem[edit]
Combinatorial computation of the distributions[edit]
Some of the results mentioned above can be derived by giving exact formulas for the probability of hitting a given integer at time n, in terms of the binomial coefficients in Pascal's triangle, by a simple computation. The total number of possible trajectories up to time n is 2n
. If |k| ≤ n and k has the same parity as n then those trajectories which result in a state S
n = k at time n are exactly those which have taken (n+k)/2 times the step +1, and (n-k)/2 times the step -1 (note that S
n and n always have the same parity). For the simple random walk all of these trajectories are equally likely and the number of trajectories satisfying this is thus equal to the binomial coefficient computing the configurations of (n-k)/2 (or (n+k)/2) elements among n, and therefore:
Using the expression n!/(k!(n-k)/2!) for the binomial coefficients and the asymptotic equivalent for the factorials given by Stirling's formula, one can obtain good estimates for these probabilities for large values of .
Here is a table listing the probabilities up to n=5.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
Recurrence[edit]
Another question is the recurrence of the walk: that is, does it almost surely return only finitely many or infinitely many times to a given state (in the first case it is said to be transient, in the second recurrent). An equivalent phrasing is: how many times will a random walk pass through a given integer if permitted to continue walking forever? A simple random walk on will cross every point an infinite number of times, that is the simple random walk on the integers is recurrent. This result has many names: the level-crossing phenomenon, recurrence or the gambler's ruin. The reason for the last name is as follows: a gambler with a finite amount of money will eventually lose when playing a fair game against a bank with an infinite amount of money. The gambler's money will perform a random walk, and it will reach zero at some point, and the game will be over.
The proof of recurrence follows immediately from the estimate of the return probability by the local central limit theorem, and the Borel-Cantelli lemma
Hitting times[edit]
If a and b are positive integers, then the expected number of steps until a one-dimensional simple random walk starting at 0 first hits b or −a is ab. The probability that this walk will hit b before −a is , which can be derived from the fact that simple random walk is a martingale.
General walks[edit]
As a Markov chain[edit]
A more sophisticated equivalent definition of a symmetric random walk on is a symmetric Markov chain with state space . For example the simple random walk is the Markov chain whose transition probabilities are .
Lattice random walk[edit]
A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. In a simple random walk, the location can only jump to neighboring sites of the lattice, forming a lattice path. In simple symmetric random walk on a locally finite lattice, the probabilities of the location jumping to each one of its immediate neighbours are the same. The best studied example is of random walk on the d-dimensional integer lattice (sometimes called the hypercubic lattice) .[1]
Higher dimensions[edit]
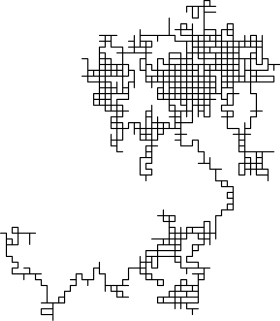


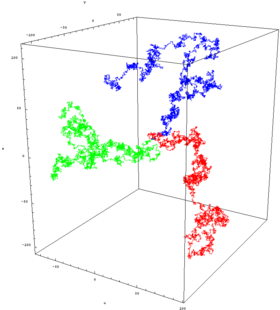
In higher dimensions, the set of randomly walked points has interesting geometric properties. In fact, one gets a discrete fractal, that is, a set which exhibits stochastic self-similarity on large scales. On small scales, one can observe "jaggedness" resulting from the grid on which the walk is performed. Two books of Lawler referenced below are a good source on this topic. The trajectory of a random walk is the collection of points visited, considered as a set with disregard to when the walk arrived at the point. In one dimension, the trajectory is simply all points between the minimum height and the maximum height the walk achieved (both are, on average, on the order of √n).
To visualize the two dimensional case, one can imagine a person walking randomly around a city. The city is effectively infinite and arranged in a square grid of sidewalks. At every intersection, the person randomly chooses one of the four possible routes (including the one originally traveled from). Formally, this is a random walk on the set of all points in the plane with integer coordinates.
Will the person ever get back to the original starting point of the walk? This is the 2-dimensional equivalent of the level crossing problem discussed above. It turns out that the person almost surely will in a 2-dimensional random walk, but for 3 dimensions or higher, the probability of returning to the origin decreases as the number of dimensions increases. In 3 dimensions, the probability decreases to roughly 34%.[2]
GGGUHHHAs a direct generalization, one can consider random walks on crystal lattices (infinite-fold abelian covering graphs over finite graphs). Actually it is possible to establish the central limit theorem and large deviation theorem in this setting.[3][4]
Random walks on graphs[edit]
Setting[edit]
Let be an undirected graph: the set is the set of vertices of , and the set of edges is a symmetric subset of (that is if and only if ); two vertices are adjacent or neighbours whenever they are joined by an edge, meaning that . The degree of a vertex is the number of incident edges: we use the notation for the degree of , which is equal to the number of edges (plus one if : a loop is considered to be twice incident to its base vertex).
A Markov chain on is a random process which can be described in the following way: for any two vertices there is a transition probability so that these satisfy that , and an initial state (a probability measure on ). The random walk is a sequence of random variables with values in , such that the law of is and the law of is specified by the conditional probabilities . Such a chain is called reversible (or time-symmetric) if there exists a function such that for all . Suppose that the Markov chain is reversible and in addition that whenever (in this case it is called a nearest neighbour chain). Then there is a nice geometric interpretation for the process: label each edge between vertices with the number (by the reversibility condition this does not depend on the order pf ); if the probability that , for a vertex adjacent to via an edge , is equal to . The term random walk is often reserved to these processes, though the nearest neighbour condition is often dropped as it is not important for the class of processes defined. The triple is called a network as it can be used to model an electrical network.
A graph is called locally finite if any vertex has finite degree. On such a graph there is a natural random walk, the simple random walk, which is defined by taking for all edges, or equivalently is the Markov chain with . Informally this is the random walk which at each step chooses a neighbour at random with the same property for each.
Properties[edit]
If is a random walk on a graph of which are vertices, then the probability for is the conditional probability that knowing that . So , and in general
(the sum is over all paths from to in ), that is the summation indices satisfy for all ).
The most basic property of a Markov chain is irreduciblity: informally this means that any given state is accessible in finite time from any other state; for a random walk it means that the probability that at some time the walk passes through any given vertex is positive (independently of the initial distribution). With the terminology above it can be stated as . If the walk is not irreducible its state space can always be decomposed into irreducible components and studied independently on those. A simple way to see if a random walk on a graph is irreducible is to delete from a graph all edges with ; if the resulting graph is connected then the walk is irreducible. A simple random walk on a connected graph is always irreducible.
An ireducible random walk is said to be recurrent if it returns infinitely many times to any given vertex (for a simple walk this does not depend on the chosen vertex); this is equivalent to . Otherwise the random walk is said to be transient, equivalently it almost surely leaves any given finite subset. A graph is said to be transient or recurrent according to whether the simple random walk has the corresponding property. The random walk on a finite graph is always recurrent. The simple random walk on a -dimensional lattice is recurrent if and only if ("Polyá's theorem"). The simple random walk on a regular (infinite) tree is always transient. The spectral radius of an irreducible random walk is defined by:
which does not depend on the initial distribution or the vertex . If then the walk is transient: the converse is not true, as illustrated by the random walk on the 3-dimensional lattice.
Random walks are better-behaved than more general Markov chains. Random walks on graphs enjoy a property called time symmetry or reversibility. Roughly speaking, this property, also called the principle of detailed balance, means that the probabilities to traverse a given path in one direction or in the other have a very simple connection between them (if the graph is regular they are in fact equal). This property has important consequences.[which?]
The basic paradigm of the study of random walks on graphs and groups is to relate graph-theoretical properties (or algebraic properties in the group case) to the behaviour of the random walk. Particularly simple examples are the detection of irreducibility by connectedness and of transience by the spectral radius given above, but there are many more subtler relations.
Random walk on a finite graph[edit]
If the graph is finite, that is its vertex set is finite, then a random walk on is a Markov chain with finite state space, and as such it is represented by a stochastic matrix with entries indexed by : the entry corresponding to a pair of vertices is the transition probability . In the case of a simple random walk on a -regular graph the matrix is equal to times the incidence matrix of the graph. If the distribution of is represented by a vector with entries indexed by summing to 1, then the distribution of is described by the vector .
There are two problems which are studied specifically in the context of the random walk on finite graphs: the study of convergence to the equilibrium state of the walk (the stationary measure) and the expected time it takes for the walk to visit all vertices (the cover time). The latter notion is intuitively obvious and can be easily formalised. The former deserves a more detailed commentary. A measure on is said to be stationary for the random walk if for all , , in other words is a fixed vector of the matrix , and informally if the initial distribution is then it remains so for all time. On any finite graph there is a unique stationary probability measure which gives the vertex the mass where is the total degree: on a regular graph this is the uniform distribution. If the graph is not bipartite then the distribution converges to the stationary measure for any initial distribution ; on a bipartite class the random walk may oscillate between the two colours of vertices. Once the limiting distribution is known it is natural to ask how fast the convergence is. This is done by studying the mixing rate of the random walk, which is defined (for a non-bipartite graph) by:
(there is a similar, albeit more involved definition for the bipartite case which measures the convergence rate to the limiting regime of alternating between two states).
The problem is to provide upper and lower bounds for both the cover time and the mixing rate and the cover time. There are general results in this direction, and also sharper result for certain classes of finite graphs. Some general results on the cover time are:[5]
- There are constants such that the cover time of any graph on n vertices is at most and at least (for any , for large enough one can take and ).
- The cover time of any regular graph on n vertices is at most .
The mixing rate is related to the spectral gap of the matrix . Supposing to simplify, that the matrix is symmetric (which amounts to the graph being regular) and that is not bipartite. Let be the number of vertices of ; then has eigenvalues (the last inequality being strict is a consequence of not being bipartite), and the mixing rate is equal to .[6] Thus graphs with large spectral gaps lead to faster convergence towards equilibrium: such graphs are commonly called expander graphs.
The fact that the mixing rate is smaller than 1 indicates that a random walk on a (non-bipartite) graph always converges exponentially to the stationary measure. For applications it is important to know the speed at which this convergence takes place. An often-used way of quantifying this is by using the total variation distance between the distribution at time and the limit distribution . The total variation of a function is defined by
and the problem is then to estimate precisely how fast decreases with . This decay is eventually exponential of rate , but this fast decay may take some time to kick in. This is measured by the mixing time which may be defined by:[7]
- .
The mixing time is significant only for . It is often defined for a specific value in this range, for example . The most general bounds for in the siginificant range are given by:[8]
where is the diameter of (the maximal number of edges between two vertices) and . The lower bound is far from sharp in general.
Random walk on an infinite graph[edit]
On infinite connected graphs one can study the asymptotic behaviour of trajectories. The most basic question is to establish whether the random walk is transient or recurrent. For this there is a basic criterion which can be formulated as follows: let be a network, fix any vertex and let be an antisymmetric function on (that is, ) such that for all and such a function is called a flow from to infinity). Then the random walk is transient if and only if there exists such a function which also has finite energy in the sense that ; this criterion does not depend on the base vertex .[9][10]
Applications of this include proving Pólya's theorem without computing the return probabilities, and proving that the simple random walk on an infinite tree is transient. More generally, the last result is true more generally for (non-elementary) hyperbolic graphs, a vast class including for example the skeletons of tessellations of the hyperbolic plane.[11]
Once the random walk is known to be transient more precise questions can be asked. First, how fast does it escape to infinity? The roughest estimate of this escape rate is its linear speed given by:
- .
We say that the walk has a linear escape rate if this is positive, sublinear otherwise. The spectral radius detects graphs with a linear escape rate:[12][13]
- A random walk has a linear escape rate if .
This implies that simple random walks on trees and hyperbolic graphs have a linear rate of escape.
Secondly, transience means that in the one-point compactification of the metric realisation of the random walk almost surely converges to the point at infinity. The natural question is whether there exists finer compactifications in which the random walk converges almost surely to a point of the boundary. The notion of Poisson boundary gives a measure-theoretic context to work on this problem. In many cases where the spectral radius is 1 (for example Pólya's walk) the Poisson boundary is trivial and brings no new information. In other cases it is nontrivial and can be realised as a topological compactification, the Martin compactification.[14] For example:
- In a regular tree, the simple random walk almost surely converges to an end;[15]
- In a regular hyperbolic graph, the simple random walk almost surely converges to a point in the Gromov boundary;[16]
Random walk on random graphs[edit]
This section may be confusing or unclear to readers. In particular, no definitions. (August 2016) |
If the transition kernel is itself random (based on an environment ) then the random walk is called a "random walk in random environment". When the law of the random walk includes the randomness of , the law is called the annealed law; on the other hand, if is seen as fixed, the law is called a quenched law. See the book of Hughes, the book of Revesz, or the lecture notes of Zeitouni.
In the context of Random graphs, particularly that of the Erdős–Rényi model, analytical results to some properties of random walkers have been obtained. These include the distribution of first[17] and last hitting times[18] of the walker, where the first hitting time is given by the first time the walker steps into a previously visited site of the graph, and the last hitting time corresponds the first time the walker cannot perform an additional move without revisiting a previously visited site.
Random walks on groups[edit]
Setting[edit]
Let be a group and and a probability measure on . Suppose that is symmetric, that is for all . Then a random walk on with step distribution is a Markov chain on with transition probabilities . In other words the probability of jumping from to is equal to . Such a process is always reversible, in fact it is symmetric since
- .
It is irreducible if and only if the support of generates . An important property is that the step distribution is -invariant, that is ; this implies for example that the behaviour is exactly the same for any starting point.
Still another interpretation is as a random walk on the Cayley graph of with respect to the support of , with probability associated to the edge . In case is the uniform probability on a symmetric generating set for the walk is the simple random walk on the Cayley graph of and is called the simple random walk on .
Random walk on a finite group[edit]
Because of transitivity, random walks on finite groups are better behaved than random walks on more general graphs. In addition the group structure can be used to prove better results than in the general transitive case, or used to great effect in special cases. Examples include:
- Cayley graphs of simple groups are very often (conjecturally always) good expanders.[19]
- Spectral estimates for convergence to the stationary measure are more precise than in general.[20]
An important phenomenon for large finite groups, discovered by Diaconis and Bayer, is the cutoff phenomenon: in some families of groups with cardinality going to infinity, well-chosen simple random walks exhibit an abrupt behaviour, meaning that until a certain time the distance to the stationary measure remain constant, after which it starts decreasing fast.[21] Conjecturally this should be a generic phenomenon; there are various special cases where it is known to take place, with explicit estimates for the decay after the cutoff time.[22][23]
Random walks on discrete groups[edit]
As in the finite case, it is possible to prove general results for simple random walks on finitely generated groups which are unattainable in a more general setting. For example:
- The random walk on an infinite group is transient if and only if the group is not commensurable to or .
- (Kesten's theorem) The spectral radius is equal to 1 if and only if the group is amenable.[24]
The theory of the Poisson boundary is particularly developed for discrete groups.
Random products of matrices[edit]
Suppose that is a measure on the linear group and let be the random walk with step distribution and initial distribution supported at the identity matrix. Then is just a product of matrices chosen independently randomly according to the law . The additional linear structure allows to define the norm of a matrix (for example the operator norm), or the matrix coefficients (linear functionals of the colums) and it is natural to ask the following questions:
- What is the asymptotic behaviour of the nrom ?
- What is the asymptotic behaviour of the matrix coefficients?
Under reasonable hypotheses there are very precise answers to these two questions, in particular analogues of the law of large numbersn central limit theorem, large deviation principle and law of the iterated logarithm.[25]
- ^ Révész Pal, Random walk in random and non random environments, World Scientific, 1990
- ^ Pólya's Random Walk Constants
- ^ M. Kotani, T. Sunada (2003). "Spectral geometry of crystal lattices". Contemporary. Math. Contemporary Mathematics. 338: 271–305. doi:10.1090/conm/338/06077. ISBN 9780821833834.
- ^ M. Kotani, T. Sunada (2006). "Large deviation and the tangent cone at infinity of a crystal lattice". Math. Z. 254 (4): 837–870. doi:10.1007/s00209-006-0951-9.
- ^ Lovász 1996, Theorem 2.1.
- ^ Lovász 1996, Corollary 5.2.
- ^ Lyons & Peres 2016, Chapter 13.3.
- ^ Lyons & Peres 2016, Corollary 13.6.
- ^ Woess 2000, Theorem 2.12.
- ^ Lyons & Peres 2016, Theorem 2.11.
- ^ Lyons & Peres 2016, Theorem 2.19.
- ^ Woess 2000, Proposition 8.2.
- ^ Lyons & Peres 2016, Proposition 6.9.
- ^ Woess, 2000 & Theorem 24.10.
- ^ Woess 2000, Theorem 26.2.
- ^ Woess 2000, Theorem 27.1.
- ^ Tishby, Biham, Katzav (2016), The distribution of first hitting times of random walks on Erdős-Rényi networks, arXiv:1606.01560.
- ^ Tishby, Biham, Katzav (2016), The distribution of path lengths of self avoiding walks on Erdős-Rényi networks, arXiv:1603.06613.
- ^ Breuillard 2014.
- ^ Saloff-Coste 2004, Theorem 5.2.
- ^ Saloff-Coste, 2004 & Definition 3.3.
- ^ Bayer, Dave; Diaconis, Persi (1992). "Trailing the dovetail shuffle to its lair". The Annals of Applied Probability. 2 (2): 294–313. doi:10.1214/aoap/1177005705. JSTOR 2959752. MR 1161056.
- ^ Saloff-Coste, 2004 & Theorem 10.4.
- ^ Breuillard 2014, Theorem 1.9.
- ^ Benoist & Quint 2016.
References[edit]
- Benoist, Yves; Quint, Jean-François (2016). "Random walks on reductive groups" (PDF). Retrieved August 28, 2016.
- Breuillard, Emmanuel (2014). "Expander graphs, property (τ) and approximate groups". In Bestvina, Mladen; Sageev, Michah; Vogtmann, Karen (eds.). Geometric group theory (PDF). IAS/Park City mathematics series. Vol. 21. American Math. Soc. pp. 325–378.
- Lovász, Laszlo (1996). "Random Walks on Graphs: A Survey". In Miklós, D.; Sós, V. T.; Szõnyi, T. (eds.). Combinatorics, Paul Erdõs is Eighty, Vol. 2 (PDF). János Bolyai Mathematical Society, Budapest. pp. 353–398.
{{cite book}}: CS1 maint: multiple names: authors list (link)
- Saloff-Coste, Laurent (2004). "Random walks on finite groups". Probability on discrete structures (PDF). Encyclopaedia Math. Sci. Vol. 110. Springer, Berlin. pp. 263–346.
- Lyons, Russell; Peres, Yuval (2016). Probability on Trees and Networks. Cambridge University Press, New York. pp. xvi+699. ISBN 9781107160156.
- Woess, Wolfgang (2000). Random Walks on Infinite Graphs and Groups. Cambridge tracts in mathematics. Vol. 138. Cambridge University Press. ISBN 0-521-55292-3.























![{\displaystyle P[S_{0}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4fec1fd8784c3de7c8b113f7ff728db75c8f584)
![{\displaystyle 2P[S_{1}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c61317a7c5e847ee2756e0a746abee7bdd9da12)
![{\displaystyle 2^{2}P[S_{2}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9583c3e61f6b6739502821af6cb79fae46f22e)
![{\displaystyle 2^{3}P[S_{3}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283a77c450ba9f63e54a01a94fb9cec8e8ee07b8)
![{\displaystyle 2^{4}P[S_{4}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208950bbe9ff3b0dd09b94b35dd390d3ddefea15)
![{\displaystyle 2^{5}P[S_{5}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b86e6675acd3df11dbd6fd80d3e1c0b10e3b6bf)

































































































![{\displaystyle \liminf _{t\to +\infty }\left({\frac {1}{t}}\mathbb {E} (d(x_{0},X_{t})\right)\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/480fb2dce3974b7a14ec19182a8c45b233744515)















