User:Halibutt/Spacetime/Relativity of simultaneity
Relativity of simultaneity[edit]
Click here for a brief section summary
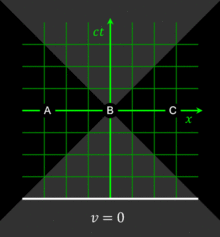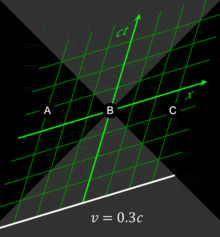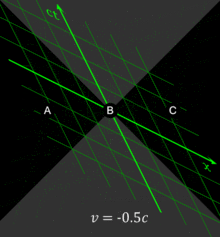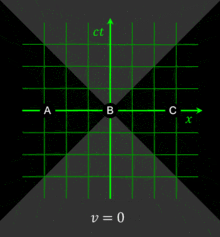
All observers will agree that for any given event, an event within the given event's future light cone occurs after the given event. Likewise, for any given event, an event within the given event's past light cone occurs before the given event. The before-after relationship observed for timelike-separated events remains unchanged no matter what the reference frame of the observer, i.e. no matter how the observer may be moving. The situation is quite different for spacelike-separated events. Fig. 2‑4 was drawn from the reference frame of an observer moving at v = 0. From this reference frame, event C is observed to occur after event O, and event B is observed to occur before event O. From a different reference frame, the orderings of these non-causally-related events can be reversed. In particular, one notes that if two events are simultaneous in a particular reference frame, they are necessarily separated by a spacelike interval and thus are noncausally related. The observation that simultaneity is not absolute, but depends on the observer's reference frame, is termed the relativity of simultaneity.[1]
Fig. 2-6 illustrates the use of spacetime diagrams in the analysis of the relativity of simultaneity. The events in spacetime are invariant, but the coordinate frames transform as discussed above for Fig. 2‑3. The three events (A, B, C) are simultaneous from the reference frame of an observer moving at v = 0. From the reference frame of an observer moving at v = 0.3 c, the events appear to occur in the order C, B, A. From the reference frame of an observer moving at v = −0.5 c, the events appear to occur in the order A, B, C. The white line represents a plane of simultaneity being moved from the past of the observer to the future of the observer, highlighting events residing on it. The gray area is the light cone of the observer, which remains invariant.
A spacelike spacetime interval gives the same distance that an observer would measure if the events being measured were simultaneous to the observer. A spacelike spacetime interval hence provides a measure of proper distance, i.e. the true distance = Likewise, a timelike spacetime interval gives the same measure of time as would be presented by the cumulative ticking of a clock that moves along a given world line. A timelike spacetime interval hence provides a measure of the proper time = .[2]: 220–221
Invariant hyperbola[edit]
Click here for a brief section summary
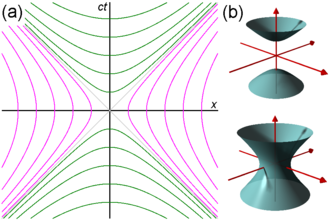
In Euclidean space (having spatial dimensions only), the set of points equidistant (using the Euclidean metric) from some point form a circle (in two dimensions) or a sphere (in three dimensions). In (1+1)-dimensional Minkowski spacetime (having one temporal and one spatial dimension), the points at some constant spacetime interval away from the origin (using the Minkowski metric) form curves given by the two equations
- with some positive real constant.
These equations describe two families of hyperbolae in an x–ct spacetime diagram, which are termed invariant hyperbolae.
In Fig. 2‑7a, each magenta hyperbola connects all events having some fixed spacelike separation from the origin, while the green hyperbolae connect events of equal timelike separation.
Fig. 2‑7b reflects the situation in (1+2)-dimensional Minkowski spacetime (one temporal and two spatial dimensions) with the corresponding hyperboloids. Each timelike interval generates a hyperboloid of one sheet, while each spacelike interval generates a hyperboloid of two sheets.
The (1+2)-dimensional boundary between space- and timelike hyperboloids, established by the events forming a zero spacetime interval to the origin, is made up by degenerating the hyperboloids to the light cone. In (1+1)-dimensions the hyperbolae degenerate to the two grey 45°-lines depicted in Fig. 2‑7a.
Note on nomenclature: The magenta hyperbolae, which cross the x axis, are termed timelike (in contrast to spacelike) hyperbolae because all "distances" to the origin along the hyperbola are timelike intervals. Because of that, these hyperbolae represent actual paths that can be traversed by (constantly accelerating) particles in spacetime: between any two events on one hyperbola a causality relation is possible, because the inverse of the slope –representing the necessary speed– for all secants is less than . On the other hand, the green hyperbolae, which cross the ct axis, are termed spacelike, because all intervals along these hyperbolae are spacelike intervals: no causality is possible between any two points on one of these hyperbolae, because all secants represent speeds larger than .
Time dilation and length contraction[edit]
Click here for a brief section summary
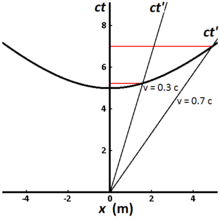
Fig. 2-8 illustrates the invariant hyperbola for all events that can be reached from the origin in a proper time of 5 meters (approximately 1.67×10−8 s). Different world lines represent clocks moving at different speeds. A clock that is stationary with respect to the observer has a world line that is vertical, and the elapsed time measured by the observer is the same as the proper time. For a clock traveling at 0.3c, the elapsed time measured by the observer is 5.24 meters (1.75×10−8 s), while for a clock traveling at 0.7c, the elapsed time measured by the observer is 7.00 meters (2.34×10−8 s). This illustrates the phenomenon known as time dilation. Clocks that travel faster take longer (in the observer frame) to tick out the same amount of proper time, and they travel further along the x–axis than they would have without time dilation.[2]: 220–221 The measurement of time dilation by two observers in different inertial reference frames is mutual. If observer O measures the clocks of observer O′ as running slower in his frame, observer O′ in turn will measure the clocks of observer O as running slower.

Length contraction, like time dilation, is a manifestation of the relativity of simultaneity. Measurement of length requires measurement of the spacetime interval between two events that are simultaneous in one's frame of reference. But events that are simultaneous in one frame of reference are, in general, not simultaneous in other frames of reference.
Fig. 2-9 illustrates the motions of a 1 m rod that is traveling at 0.5 c along the x axis. The edges of the blue band represent the world lines of the rod's two endpoints. The invariant hyperbola illustrates events separated from the origin by a spacelike interval of 1 m. The endpoints O and B measured when t′ = 0 are simultaneous events in the S′ frame. But to an observer in frame S, events O and B are not simultaneous. To measure length, the observer in frame S measures the endpoints of the rod as projected onto the x-axis along their world lines. The projection of the rod's world sheet onto the x axis yields the foreshortened length OC.[3]: 125
(not illustrated) Drawing a vertical line through A so that it intersects the x' axis demonstrates that, even as OB is foreshortened from the point of view of observer O, OA is likewise foreshortened from the point of view of observer O′. In the same way that each observer measures the other's clocks as running slow, each observer measures the other's rulers as being contracted.
- ^ Savitt, Steven. "Being and Becoming in Modern Physics. 3. The Special Theory of Relativity". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 26 March 2017.
- ^ a b Cite error: The named reference
Schutzwas invoked but never defined (see the help page). - ^ Cite error: The named reference
Collierwas invoked but never defined (see the help page).





