Talk:Permutohedron

A fact from Permutohedron appeared on Wikipedia's Main Page in the Did you know column on 17 August 2007. The text of the entry was as follows:

Did you know... that the six permutations of the vector (1,2,3) form a hexagon in 3d space, the 24 permutations of (1,2,3,4) form a truncated octahedron in four dimensions, and both are examples of permutohedra?

A record of the entry may be seen at Wikipedia:Recent additions/2007/August.

Wikipedia

Zonotopes[edit]

The article claims that every permutohedron is a zonotope. This is morally true, but unfortunately a zonotope is defined to be a 3-dimensional thing, while a permutohedron can be n-dimensional for any n. This can't be fixed in the permutohedron article, it needs to be fixed in the zonotope article. Adam1729 01:16, 17 August 2007 (UTC)[reply]

Actually, I think that's a misreading of the zonotope article (a redirect to zonohedron): it defines a zonohedron as a three-dimensional thing, and a zonotope as arbitrary dimensional. But the zonotope definition was buried in the middle of the article; I just made it more prominent. —David Eppstein 04:08, 18 August 2007 (UTC)[reply]

Thanks. The confusion is partly because a ...hedron is 3d whereas a ...tope is n-d, except for a permutohedron. Maybe we should say this. Adam1729 01:12, 19 August 2007 (UTC)[reply]

Another, closely related exception: associahedron. Arcfrk 05:19, 22 August 2007 (UTC)[reply]

Omnitruncated n-simplices[edit]

By induction I believe this is true, even if no sources to support it:

The permutohedron of order n is an omnitruncated (n − 1)-simplex.:

Omnitruncated n-simplices
n	Uniform polytope (Omnitruncated (n-1)-simplex) Schläfli symbol group: Coxeter-Dynkin diagram	Coxeter plane projection	Picture	Tessellation A^~_n-1 or P_n Coxeter group	Vertices n!	Facets 2ⁿ-2	Facet counts by type
2	Interval t₀{} A₁:			Apeirogon	2	2
3	Hexagon (Truncated triangle) t_0,1{3} A₂:			Hexagonal tiling	6	6	2*3 {}
4	Truncated octahedron (Omnitruncated tetrahedron) t_0,1,2{3,3} A₃:			Bitruncated cubic honeycomb	24	14	2*4 t_0,1{3} + 6 {}x{}
5	Omnitruncated 5-cell t_0,1,2,3{3,3,3} A₄:				120	30	25 t_0,1,2{3,3} + 210 t_0,1{3}x{}
6	Omnitruncated 5-simplex t_0,1,2,3,4{3,3,3,3} A₅:				720	62	26 t_0,1,2,3{3,3,3} + 215 t_0,1,2{3,3} + 20 t_0,1{3}xt_0,1{3}
7	Omnitruncated 6-simplex t_0,1,2,3,4,5{3,3,3,3,3} A₆:				5040	126	27 t_0,1,2,3,4{3,3,3,3} + 221 t_0,1,2,3{3,3,3} + 35 t_0,1,2{3,3}xt_0,1{3}
8	Omnitruncated 7-simplex t_{0,1,2,3,4,5,6}{3,3,3,3,3,3} A₇:				40320	254
9	Omnitruncated 8-simplex t_{0,1,2,3,4,5,6,7}{3,3,3,3,3,3,3} A₈:				362880	510
...
n	Omnitruncated (n-1)-simplex t_0,1,..,n-2{3^n-2} A_n-1:...				n!	2ⁿ-2	Σ[i=0..n-3] C(n,i)t_0,...,i-1{3^i-1}xt_0,...,n-2-i{3^n-2-i}

Tom Ruen (talk) 00:13, 25 November 2007 (UTC). (Expanded into a table) Tom Ruen (talk) 07:24, 10 December 2007 (UTC)[reply]

This is certainly very compelling. Perhaps one approach to prove this might be to explicate the relationship of the n-order permutohedron with the n-hypercube: Note, for example, that the line segment is the intersection of a square with a diagonal line at the appropriate depth from one of its vertices. The hexagon is the intersection of a cube with the plane wherein lies the permutohedron, which is at an appropriate depth from one of the cube's corners. I surmise that the truncated octahedron (omnitruncated tetrahedron) is the intersection of the corresponding hyperplane with the 4-cube at the appropriate depth. Now, the key to these observations is that truncating a corner of the n-cube yields an (n-1)-simplex, but if the truncating plane is moved deeper into the cube, eventually the simplex will intersect with other cube facets and thereby become truncated, rectified, and eventually omnitruncated(?). So if we can prove that the hyperplane that an n-permutohedron lies in is precisely the depth at which the (n-1)-simplex is omnitruncated, then we have established your conjecture.—Tetracube (talk) 00:24, 14 August 2008 (UTC)[reply]

Yes, it does look like an order-n permutohedron is constructed on the hyperplane cross-section (n+1)-hypercube. The hyperplane is contained by the hypercube center and appears to pass through the center of a set of ridges of each hypercube: vertices of square, mid-edges of cube, and mid-faces of tesseract, and mid-cells of penteract. But just a guess! Tom Ruen (talk) 04:24, 14 August 2008 (UTC)[reply]

I think this misses the point. We shouldn't be making and then trying to prove conjectures here, per WP:NOT. Not even on the talk page. We should be trying to determine whether someone else has already established this, and only if we can find appropriate reliably published sources should we add this to the article. —David Eppstein (talk) 00:55, 14 August 2008 (UTC)[reply]

Hmmmm, perhaps this wiki-talk page will inspire a paper to be published that will prove it? At least that was my secret inspiration to putting it here. :) My table seems defendable on this talk page, even if discussion on proving it doesn't, oops. For me, a computational construction would be a proof. We can compute and omnitruncated simplices from a Wythoff construction, and permutohedron vertices constructable via permutations of coordinates, and facets by a convex hull, and elements can be counted. If these are computed and vertices match to any level desired, that's a proof to me (or counter proof if wrong of course.) Anyway, from the papers I've seen, there's been nothing in this direction, all abstract stuff. :( Tom Ruen (talk) 04:24, 14 August 2008 (UTC)[reply]

I have found a proof for this conjecture. The key observation lies in the fact that an omnitruncated n-simplex occurs as corner facets in an omnitruncated (n+1)-cube. There is a trivial mapping from the Cartesian coordinates of the corner facet of an omnitruncated n-cube to a permutohedron of order n, thereby establishing the equivalence. However, since this is likely to be original research, I'm refraining from posting the proof here (I've emailed it to Tom Ruen for verification).—Tetracube (talk) 19:14, 25 November 2008 (UTC)[reply]

I got Tetracube's email, but don't have time now to try to follow it, but I see no problem having it posted here on the talk page. Tom Ruen (talk) 03:40, 26 November 2008 (UTC)[reply]

Hi Tom Ruen, I've found an elegant proof of your conjecture that the order-n permutohedron is an omnitruncated simplex. I'm not sure if this would be Original Research, so I'm refraining from posting this on Wikipedia for now, but I thought you might be interested in it. The key observation is that the omnitruncated n-simplex occurs as facets in an omnitruncated (n+1)-cube. In particular, it occurs in the "diagonal" position, in the positions parallel to the hyperplanes of the (n+1)-cross's facets (i.e., correponding to the vertices of an n-cube). The Cartesian coordinates of an omnitruncated n-cube can be obtained as follows: - We generate an n-dimensional base point based on the following steps, and then take all permutations of coordinates and sign (equivalent to reflecting across the mirrors corresponding with the Dynkin symbol for the n-cube). - In 1D, the point is simply <1>. - In n dimensions, we obtain the base point by appending the sum of the largest coordinate in the previous dimension with √2. For example, in 2D, our base point is <1, 1+√2>, which generates the octagon, and in 3D, our base point is <1, 1+√2, 1+2√2>, which generates the great rhombicubotahedron, and in 4D, <1, 1+√2, 1+2√2, 1+3√2> generates the omnitruncated tesseract. The diagonal facet of an omnitruncated n-cube is simply the convex hull of all permutations of the base point, but without permutation of sign (i.e., take all non-negative coordinates only). Now, since the shape of the convex hull of these points is invariant under translation and scaling, we may subtract <1,1,1,...,1> and reduce the coordinates to permutations of <0, √2, 2√2, 3√2, ..., n√2>. Then, dividing by √2, we get permutations of <0, 1, 2, 3, ..., n>. This is the permutohedron of order n. QED. --T

This week I was generating coordinates for the truncations of the regular n-simplices, and found Tetracube's page User:Tetracube/Uniform_polytera for n-orthoplexes, and realized the n-simplices could be generated in (n+1)-space as facets, and this inductive enumeration shows the Omnitruncated n-simplex is a representation of the 'n-permutohedron, and the lower truncation forms come out equally with permutations filtered by repeating coordinates of smaller integers of unringed nodes. Anyway, pretty cool, proved in my mind, sources or not: User:Tetracube/Uniform_polytera#Simplex coordinates Tom Ruen (talk) 03:48, 28 July 2010 (UTC)[reply]

Conway says the "dual lattice" A_n^* Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9., p 115, has Voronoi cells as permutohedra, and defines as the union of all A_n lattices, (n+1) positions of single ringed Coxeter diagrams, and this apparently is equivalent to the dual honeycomb of the omnitruncation (one fulled ringed Coxeter Diagram). Tom Ruen (talk) 02:37, 30 July 2012 (UTC)[reply]

Spelling[edit]

In math literatute I've usually seen the term spelled "permutAhedron". Why is it "permutOhedron" here? Maybe my sample is biased, but is there any particular reason either way? I'd think, at the least, the opening sentence should have both spellings. Zaslav (talk) 04:46, 25 June 2011 (UTC)[reply]

I think the "o" spelling is a little more common, and matches the original French spelling, so I it makes sense to keep it as the primary spelling. But I agree that there seems to be enough disagreement over this point to include the other spelling as a valid variant, so I've gone ahead and added it to the lede. —David Eppstein (talk) 05:09, 25 June 2011 (UTC)[reply]

I have great respect for David Eppstein, but he seems to be backing a losing horse in this matter. I just did a Google search, and this Wikipedia page was the only hit that preferred the spelling with an "o"; one other page gave both, but preferred "a"; the other 28 used only "a". LyleRamshaw (talk) 01:05, 25 February 2017 (UTC)[reply]

I see 827 for A and 759 for O in Google scholar, not enough of a difference to be meaningful. I think scholar is more relevant than general web searches for this topic. And if your Google search found only 29 hits, something is wrong. —David Eppstein (talk) 02:04, 25 February 2017 (UTC)[reply]

5 years later, and they still seem to be neck and neck. MathSciNet has 101 "permutahedron" hits and 97 "permutohedron" hits. Personally I agree with David, but it's probably just a bias in the literature I'm familiar with. I think it's handled well in any case. 172.250.24.180 (talk) 04:50, 17 August 2022 (UTC)[reply]

Incidentally, Google scholar also has 2820 hits for "literatute", more than both spellings combined. (Sorry, Z, no intention of criticizing you for the sort of typo we all make, just amused by this instance of Muphry's law.) —David Eppstein (talk) 06:55, 17 August 2022 (UTC)[reply]

OEIS A019538[edit]

Triangle OEIS: A019538:

Number of set compositions (ordered set partitions) of n items into k parts. Number of k dimensional 'faces' of the n dimensional permutohedron (see Simion, p. 162). - Mitch Harris, Jan 16 2007

I think that this description of the triangle in the OEIS contains two mistakes: It actually is the number of n-k-dimensional faces, and it is the permutohedron of order n (or the n-1-dimensional permutohedron). It's difficult to correct stuff there. Maybe this mistake should be mentioned in references to this sequence. Watchduck (quack) 23:38, 9 August 2013 (UTC)[reply]

   k = 1    2    3    4    5
n
1      1                               1
2      1    2                          3
3      1    6    6                    13
4      1   14   36   24               75
5      1   30  150  240  120         541

I just corrected it in the OEIS: Number of (n-k)-dimensional 'faces' of the permutohedron of order n (i.e. the (n-1)-dimensional permutohedron).
In case there is any discussion, here is an example for n=4:
The permutohedron of order 4 (i.e. the 3-dimensional permutohedron) is the truncated octahedron.
It has 1 cell (3-dimensional face), 14 faces (2-dimensional faces), 36 edges (1-dimensional faces), 24 vertices (0-dimensional faces) Watchduck (quack) 19:07, 29 October 2014 (UTC)[reply]

The dimension of this figure is ambiguous. The system of coordinates by which it is defined are n-dimensional, but it lives within an (n − 1)-dimensional hyperplane within the n-dimensional space. —David Eppstein (talk) 19:28, 29 October 2014 (UTC)[reply]

Changed it to "...of order n (an (n-1)-dimensional polytope)". Watchduck (quack) 22:17, 29 October 2014 (UTC)[reply]

That sounds good to me. —David Eppstein (talk) 23:13, 29 October 2014 (UTC)[reply]

New image[edit]

For a project at University, I've edited the main file of this article changing the edges' color so that they are not mistaken any more. I'm not sure whether changing it or leaving the old one. Maybe you @Watchduck: can tell me what to do... Jordiventura96 (talk) 00:24, 6 January 2020 (UTC)[reply]

What are the edge colors supposed to indicate? It's obviously not whether edges are parallel to each other. In general I think both images have a lot of visual clutter that doesn't really add much to understanding of the concept of a permutohedron. Imagine if you tried to read the previous sentence with the letters randomly colored red, blue, and green — would that make it easier to read? File:Permutohedron.svg is significantly less cluttered. —David Eppstein (talk) 00:59, 6 January 2020 (UTC)[reply]

@Jordiventura96: The edge colors in my file indicate which digit of the left inversion count changes, and it says so in the description. I have no idea what the edge colors in your image are supposed mean - not to mention what the connection to the same colors in the inversion counts is supposed to be. Do you claim that your image expresses some relevant meaning in its current form? Then please give a meaningful description on its page. Otherwise I suggest to modify or delete it.

The edge colors are not "mistaken", as some IP claimed ten month ago. It is simply not the Cayley graph (which is also shown in the article).

@David Eppstein: In the plain version it is not obvious why there is an edge between two permutations, so I included the inversion counts, where an edge corresponds to the increase of one digit. I would not choose that as an example, if I wanted to explain what visual clutter is... But yes, maybe the intro image should not use such an abstract concept as the inversion count. I suggest replacing it by a version where the edge color indicates which pair of places is swapped. (In the bottom vertex of an edge the elements on those two places are in natural order.) It shows which edges are parallel to each other, which is relevant information about the geometric figure. Watchduck (quack) 14:45, 6 January 2020 (UTC)[reply]

The reasons for the edges between permutations are less about combinatorial reasons (inversion counts) and more about geometric reasons (e.g. the Euclidean distance between pairs of vectors that form edges is only sqrt(2), the shortest possible). —David Eppstein (talk) 17:28, 6 January 2020 (UTC)[reply]

Yes, the polytope itself does not need a notion of edges going upward. I agree with you, that my old file displays combinatorial information without geometric relevance too prominently. But in the new file one the right, combinatorial matches relevant geometric information, namely that there are 6 groups of 6 parallel edges. (Does that not illustrate how this is a zonohedron?) Watchduck (quack) 18:31, 6 January 2020 (UTC)[reply]

It makes more sense, but the colors still make it very busy for no good reason. Also, they are far far out of compliance with Wikipedia:Manual of Style/Accessibility. In particular the light cyan (1EFFE2) on white (FFFFFF) is a bad combination for contrast, as is the light pink (FF69FF) on white. The green against orange (00B300 vs FFAF00) is also a bad combination; I didn't check them all. You can check this yourself using https://snook.ca/technical/colour_contrast/colour.html —David Eppstein (talk) 18:49, 6 January 2020 (UTC)[reply]

Permutations (black) among other points in the same hyperplane

I think in the raytraced version the edges are clear enough. (The big image on the right is now that version instead of the SVG.)
I also made a version that shows the permutohedron among all points with positive integer coordinates in the same hyperplane. Watchduck (quack) 01:33, 18 January 2020 (UTC)[reply]

Expansion of the intro[edit]

I think since 52.144.34.243 started to confuse permutohedron and Cayley graph in February 2019, the intro has become more confusing than helpful. I think the version before was just fine.

The addition that the permutations can be 0-based also makes sense to me. (One could just write "permutations of the first n natural numbers".)

Right now the old intro is followed by a sentence to the effect, that the elements of the permuted vector can be any rational numbers. Such a generalized permutohedron could be described in the article, if relevant. But I don't think it belongs in the intro.

The statement after that seems to originate from one added by the IP, which was:

The edge-graph of any permutohedron is the Cayley graph of S_n with respect to the generating set of adjacent transpositions (1,2), . . . , (n-1,n).

Zaslav has then gradually changed that to:

The edges of a permutohedron (of any kind) are the line segments connecting each pair of permutations that differ only by an adjacent transposition, i.e., the interchange of two adjacent coordinates.

This is clearly a confusion of the permutohedron with the related Cayley graph. At least to me an "adjacent transposition" is clearly one that swaps adjacent places.
But in the permutohedron the edges correspond to all possible transpositions. Just the swapped values are adjacent (i.e. the swapped things on these places).
Here I have written what I hope to be a clarification. (Let me know if you think it's not.)

The intro should be only about the permutohedron. I will change the article accordingly. Watchduck (quack) 20:32, 24 January 2020 (UTC)[reply]

Thanks. I agree, we should distinguish the permutohedron from the related Cayley graph. —David Eppstein (talk) 06:50, 25 January 2020 (UTC)[reply]

There is a comment on Commons that adds a new flavor of confusion to this topic: c:Category talk:Permutohedron of order 4 (raytraced) I don't think the claim that the "transposition that swaps the first, second, or final pair changes from vertex to vertex" makes sense, but maybe someone else gets what Adam is trying to say. Watchduck (quack) 11:36, 11 March 2020 (UTC)[reply]

This cannot be accurate[edit]

One sentence reads:

"More generally, V. Joseph Bowman (1972) uses that term for any polytope whose vertices have a bijection with the permutations of some set."

So, any polytope with exactly n! vertices would then be called a permutohedron???

Either 1) there is more to what Bowman (1972) proposes, or else 2) this fact is so incompatible with intelligent geometry that it does not belong in the article.216.161.117.162 (talk) 19:10, 26 September 2020 (UTC)[reply]

You didn't read the source, did you? "Definition: A permutation polyhedron of order n is a convex polyhedron whose extreme points are in one-to-one correspondence with the permutations of order n." He goes on to add a few lines down that he is only actually interested in polyhedra that are connected to optimization problems over permutations. It is used in this article only for the purpose of highlighting the ambiguity of the term "permutation polytope" and is perfectly appropriate in the article for that purpose. —David Eppstein (talk) 19:28, 26 September 2020 (UTC)[reply]

Train wreck[edit]

This article is almost incomprehensible. Here is an example of why.

The first two paragraphs of the section Vertices, edges, and facets read as follows:

"The permutohedron of order n has n! vertices, each of which is adjacent to n − 1 others, so the total number of edges is (n − 1)n!/2. Each edge has length √2, and connects two vertices that differ by swapping two coordinates the values of which differ by one.

"The permutohedron has one facet for each nonempty proper subset S of {1, 2, 3, ..., n}, consisting of the vertices in which all coordinates in positions in S are smaller than all coordinates in positions not in S. Thus, the total number of facets is 2n − 2. More generally, the faces of the permutohedron (including the permutohedron itself, but not including the empty set) are in 1-1 correspondence with the strict weak orderings on a set of n items: a face of dimension d corresponds to a strict weak ordering in which there are n − d equivalence classes. Because of this correspondence, the number of faces is given by the ordered Bell numbers."

Consider the phrase: "consisting of the vertices in which all coordinates in positions in S are smaller than all coordinates in positions not in S".

All coordinates WHERE??? No Euclidean space has been mentioned. So a reader will not have any idea of WHERE these coordinates are supposed to exist.

This is unfortunately typical of this article.65.141.95.170 (talk) 19:53, 3 November 2020 (UTC)[reply]

The coordinates are very clearly described in the second sentence of the article. —David Eppstein (talk) 20:26, 3 November 2020 (UTC)[reply]

I agree, that the section Vertices, edges, and facets (current version) is very hard to read. I will try to clarify it on the talk page, and maybe that will lead to improvements. Watchduck (quack) 23:59, 4 November 2020 (UTC)[reply]

Vertices, edges, and facets in detail[edit]

Text and explanations
The permutohedron of order n has n! vertices , each of which is adjacent to n − 1 others,
so the total number of edges is (n − 1)n!/2 .	(Based on what rule?)
Each edge has length √2, and connects two vertices
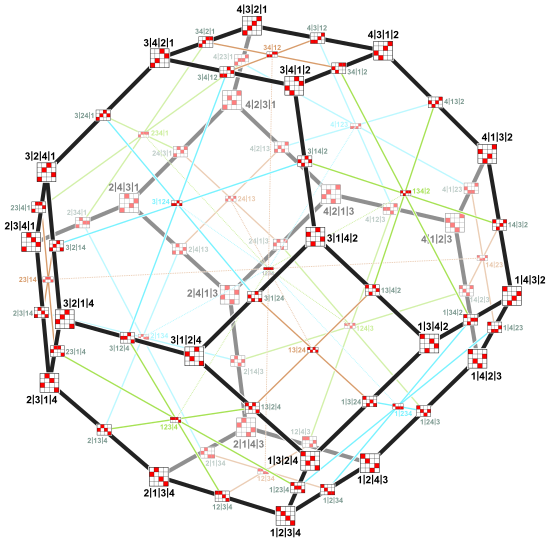
that differ by swapping two coordinates the values of which differ by one.	Green edge 123–132 in swaps 2 and 3. So does 1234–1324 in .
The permutohedron has one facet for each nonempty proper subset S of {1, 2, 3, ..., n},	Those are all subsets except the empty set and the set itself. The following files show permutohedron-like Cayley graphs. Reading the square matrices by row gives the coordinates. Reading them by column gives the corresponding permutohedron coordinates. In the facets are the 1-faces a.k.a. edges. In they are the (2-)faces (hexagons and squares). The facets are represented by two-line matrices. Their first line is the subset. E.g. in the hexagon the top edge corresponds to the subset {2} and the bottom edge to {1, 3}.
consisting of the vertices	E.g. the vertices of the hexagons and squares.
in which all coordinates in positions in S are smaller than all coordinates in positions not in S.	This is indeed difficult. First note that a coordinate is one value, not the tuple. S is the subset corresponding to the facet. Its elements are now called positions. Read the square matrices in this file by column to get the coordinates of the permutohedron. Consider the top left hexagon where S is {2}. So the positions is S are {2} and those not in S are {1, 3, 4}. Look at the six vertices. Their coordinate in position 2 is always 1, which is of course smaller than the other three. Consider the square one the left where S is {2, 3}. So the positions in S are {2, 3} and those not is S are {1, 4}. Look at the four vertices. Their coordinates on positions 2 and 3 are 1 and 2, which is smaller than those on positions 1 and 4, which are 3 and 4.
Thus, the total number of facets is 2ⁿ − 2.	The number of subsets is a power of two, and we excluded two.
More generally, the faces of the permutohedron (including the permutohedron itself, but not including the empty set) are in 1-1 correspondence with the strict weak orderings on a set of n items:	has oB(3) = 13 and has oB(4) = 75 little matrices.
a face of dimension d corresponds to a strict weak ordering in which there are n − d equivalence classes.	The equivalence classes (or blocks of the set partition) are the rows of these matrices.
Because of this correspondence, the number of faces is given by the ordered Bell numbers.	vertices, edges, facets, faces k = 1 2 3 4 5 n 1 1 1 2 1 2 3 3 1 6 6 13 4 1 14 36 24 75 5 1 30 150 240 120 541
The number of $(n-k)$ -dimensional faces in a permutohedron of order $n$ is found in the triangle $T(n,k)=k!\cdot S(n,k)$ , where $S(n,k)$ are the Stirling numbers of the second kind
(sequence A019538 in the OEIS) — shown on the right, together with its row sums, the ordered Bell numbers.

Did you not understand that just from reading this section? ;) Greetings, Watchduck (quack) 02:14, 5 November 2020 (UTC)[reply]

Rewrite[edit]

vertices, edges, facets, faces
Face dimension

d = n - k

.

   k = 1    2    3    4    5
n
1      1                               1
2      1    2                          3
3      1    6    6                    13
4      1   14   36   24               75
5      1   30  150  240  120         541

The permutohedron of order $n$ has $n!$ vertices, each of which is adjacent to $n - 1$ others. The number of edges is $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}(n − 1) n!/2$ , and their length is $\sqrt 2$ .

Two connected vertices differ by swapping two coordinates, whose values differ by 1. The pair of swapped places corresponds to the direction of the edge. (In the example image the vertices $(3, 2, 1, 4)$ and $(2, 3, 1, 4)$ are connected by a blue edge and differ by swapping 2 and 3 on the first two places. The values 2 and 3 differ by 1. All blue edges correspond to swaps of coordinates on the first two places.)

The number of facets is $2 n - 2$ , because they correspond to non-empty proper subsets $S$ of ${1 \dots n}$ . The vertices of a facet corresponding to subset $S$ have in common, that their coordinates on places in $S$ are smaller than the rest.

Facet examples
For order 3 the facets are the 6 edges, and for order 4 they are the 14 faces. The coordinates on places $i$ where $i \in S$ are marked with a dark background. It can be seen, that they are smaller than the rest. The square on top corresponds to the subset ${3, 4}$ . In its four vertices the coordinates on the last two places have the smallest values (namely 1 and 2).
order 3		order 4
1-element subsets	2-element subsets	1-element subsets	2-element subsets	3-element subsets

More generally, the faces of dimensions 0 (vertices) to $n - 1$ (the permutohedron itself) correspond to the strict weak orderings of the set ${1 \dots n}$ . So the number of all faces is the $n$ -th ordered Bell number. A face of dimension $d$ corresponds to an ordering with $k = n - d$ equivalence classes.

Face examples
order 3	order 4

The images above show the face lattices of the permutohedra of order 3 and 4 (without the empty faces). Each face center is labelled with a strict weak ordering. E.g. the square on top as 3 4 \| 1 2, which represents $({3, 4}, {1, 2})$ . The orderings are partially ordered by refinement, with the finer ones being on the outside. Moving along an edge toward the inside means merging two neighbouring equivalence classes. The vertex labels a \| b \| c \| d interpreted as permutations (a, b, c, d) are those forming the Cayley graph. The before mentioned facets are among these faces, and correspond to orderings with two equivalence classes. The first one is used as the subset $S$ assigned to the facet, so the ordering is $(S, S c)$ . The images below show how the facets of the $n$ -permutohedron correspond to the simplical projection of the $n$ -cube. The binary coordinate labels correspond to the subsets $S$ , e.g. 0011 to ${3, 4}$ . (The vertex projected to the center does not correspond to a facet. Nor does its opposite vertex in the $n$ -cube, which is not part of the projection.)

The number of faces of dimension $d = n - k$ in the permutohedron of order $n$ is given by the triangle $T$ (sequence A019538 in the OEIS):
$T(n,k)=k!\cdot \left\{{n \atop k}\right\}$ with $\textstyle \left\{{n \atop k}\right\}$ representing the Stirling numbers of the second kind
It is shown on the right together with its row sums, the ordered Bell numbers.

Added source: Lancia, Giuseppe (2018), Compact extended linear programming models, Cham, Switzerland: Springer, ISBN 978-3-319-63975-8

Why are you starting your rewrite with zero sources? All content should be based on reliable sources. That means, find sources first, then write according to what the sources say about the subject. The article in its current state is not unsourced. Any rewrite should not be a step backwards in that respect. —David Eppstein (talk) 02:21, 11 November 2020 (UTC)[reply]

I just left them out here, because I don't like stray references on talk pages. Anyway, I just added them. (And removed them again after adding the change.)

The statement that was criticized as unreadable ("consisting of the vertices in which all coordinates...") does not currently have a source. I found one here: https://www.mimuw.edu.pl/~jarekw/pdf/Permutahedron.pdf (p. 105) There are two ways to assign the subsets to the facets. I used the second block of the SWO, but this source uses the first block, and so does the current text in the article. Guess I will have to adapt to that. (Done.) --Watchduck (quack) 16:13, 15 November 2020 (UTC)[reply]

Generalized permutohedron[edit]

truncated octahedron	truncated cuboctahedron	truncated icosidodecahedron	source
descriptions in the source			source
	signed p.		This term is sometimes used for the convex hull of the signed permutations. e.g. On Flag Vectors..., Mixed volumes of hypersimplices
p. of type A₃	p. of type B₃		https://books.google.de/books?id=W_SPdwfPTw8C&pg=PA83#v=onepage&q&f=false
p. for the symmetric group S₄	p. for the hyperoctahedral group W₃	p. for W(H₃)	https://books.google.de/books?id=Y01d6g5UemQC&pg=PA135#v=onepage&q&f=false

TBC, started by Watchduck (quack) 16:57, 15 November 2020 (UTC)[reply]

Cayley graph/Permutohedron confusion[edit]

The part about "The permutohedron-like Cayley graph of S₄" and a large part of the page https://commons.wikimedia.org/wiki/Category:Permutohedron_of_order_4_(raytraced)#Permutohedron_vs._Cayley_graph is superfluous. One only needs to realize that applying a permutation on one side swaps places, and applying it on the other side swaps values. Both compared graphs are Cayley graphs, one is left-Cayley, the other is right-Cayley. Leen Droogendijk (talk) 11:08, 9 June 2021 (UTC)[reply]