Quadratische Funktion

Eine quadratische Funktion (auch ganzrationale Funktion zweiten Grades) ist eine Funktion, die als Funktionsterm ein Polynom vom Grad 2 besitzt, also von der Form
- mit
ist. Der Graph ist die Parabel mit der Gleichung . Für ergibt sich eine lineare Funktion.
Die Funktionen der Form mit (also ) heißen spezielle quadratische Funktionen. Die Funktion mit heißt Quadratfunktion.
Quadratfunktion und spezielle quadratische Funktion[Bearbeiten | Quelltext bearbeiten]
Die Funktion mit der Zuordnungsvorschrift heißt Quadratfunktion. Ihr Graph ist eine nach oben geöffnete, zur y-Achse symmetrische Parabel, deren Scheitelpunkt im Koordinatenursprung liegt, die Normalparabel.
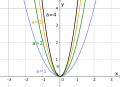
Eine Funktionen der Form mit heißt spezielle quadratische Funktion. Ihr Graph ist eine zur -Achse symmetrische Parabel mit Scheitelpunkt im Ursprung. Diese entsteht aus der Normalparabel durch Strecken oder Stauchen in Richtung der -Achse und gegebenenfalls Spiegeln an der -Achse:
- : Die Parabel ist nach oben geöffnet.
- : Die Parabel ist nach unten geöffnet.
- : Der Graph ist in Richtung der -Achse gestaucht, d. h. in der Länge zusammengedrückt, wodurch er breiter erscheint und flacher ist.
- : Der Graph ist in Richtung der -Achse gestreckt, d. h. in die Länge gezogen, wodurch er schmaler erscheint und steiler ist.
Für : ist der Graph im Vergleich zur Normalparabel einfach an der -Achse gespiegelt.
-
Spiegelung bei Vorzeichenwechsel
-
Stauchung bei
-
Streckung bei
Allgemeine quadratische Funktion[Bearbeiten | Quelltext bearbeiten]
Die Zuordnungsvorschrift der allgemeinen quadratischen Funktion ist . Die Koeffizienten , und bestimmen den Wertebereich und die Form des Graphen.
Parameter a[Bearbeiten | Quelltext bearbeiten]
Wie der Wert von die Form des Graphen verändert, kann man am besten erkennen, wenn man und setzt. Man erhält dann eine gestreckte oder gestauchte und gegebenenfalls an der -Achse gespiegelte Normalparabel.
- : Der Graph ist nach oben geöffnet.
- : Der Graph ist nach unten geöffnet.
- : Der Graph ist in Richtung der -Achse gestaucht, d. h. in der Länge zusammengedrückt, wodurch er breiter erscheint und flacher ist.
- : Der Graph ist in Richtung der -Achse gestreckt, d. h. in die Länge gezogen, wodurch er schmaler erscheint und steiler ist.
Für : ist der Graph im Vergleich zur Normalparabel einfach an der -Achse gespiegelt.
Parameter c[Bearbeiten | Quelltext bearbeiten]
Es gilt . Der Parameter ist also der -Wert des Schnittpunkts der Parabel mit der -Achse. Eine Veränderung des Parameters bewirkt eine Verschiebung in -Richtung. Wird um eins erhöht, dann wird der Graph um eine Einheit nach oben verschoben. Wird um eins verringert, wird der Graph dagegen um eine Einheit nach unten verschoben.
Parameter b[Bearbeiten | Quelltext bearbeiten]
Der Parameter gibt die Steigung der Parabel im Schnittpunkt mit der -Achse an. Insbesondere kann man am Vorzeichen von erkennen, ob die -Achse mit dem fallenden oder dem ansteigenden Ast der Parabel geschnitten wird. Hieraus lassen sich wiederum Rückschlüsse über die Zahl und die mögliche Lage von Nullstellen ziehen.
Eine Veränderung des Parameters bewirkt eine Verschiebung sowohl in - als auch in -Richtung. Wird um eins erhöht, dann wird der Graph um Einheiten nach links und nach unten verschoben. Wird um eins verringert, wird der Graph dagegen um Einheiten nach rechts und nach oben verschoben.
Scheitelpunkt[Bearbeiten | Quelltext bearbeiten]
Der Scheitelpunkt ist maßgeblich für die Lage der Parabel und repräsentiert entweder das absolute Minimum (falls positiv ist) oder das absolute Maximum (wenn negativ ist). Die Koordinaten des Scheitelpunkts lassen sich direkt ablesen, wenn der Funktionsterm in der Scheitelpunktform vorliegt:
- .
Der Scheitelpunkt hat dann die Koordinaten . Der Graph ist achsensymmetrisch zu einer Parallele zur -Achse durch .
Zur Bestimmung des Scheitelpunkts bzw. der Scheitelpunktform gibt es mehrere Methoden:
Bestimmung der Scheitelpunktform mit quadratischer Ergänzung[Bearbeiten | Quelltext bearbeiten]
Die Scheitelpunktform kann aus der Darstellung durch quadratische Ergänzung bestimmt werden.
Beispiel: Bestimmung der Scheitelform der quadratischen Funktion .
| Die ursprüngliche Funktionsgleichung | |
| Der Faktor vor dem wurde ausgeklammert, wobei das konstante Glied + 5 ausgeschlossen bleibt. | |
| Es wird eine quadratische Ergänzung zu durchgeführt. | |
| Durch die quadratische Ergänzung ist es leicht möglich, mithilfe der binomischen Formeln aus einem Teil des Terms ein Quadrat herauszuziehen. | |
| Nun wurde noch die Klammer mit dem Faktor 2 wieder aufgelöst, um den Term zu vereinfachen. | |
| In der Endform lässt sich nun der Scheitelpunkt ablesen. |
Bestimmung des Scheitelpunkts mit Hilfe der Ableitung[Bearbeiten | Quelltext bearbeiten]
Eine weitere Möglichkeit zur Berechnung des Scheitelpunktes bietet die Differentialrechnung. Da der Scheitelpunkt immer eine (lokale) Extremstelle (Maximum bzw. Minimum) ist, liefert die Nullstelle der ersten Ableitung der Funktion den -Wert des Scheitelpunktes:
- ,
Durch Einsetzen ergibt sich der -Wert:
Beispiel: Bestimmung des Scheiteilpunkts der quadratischen Funktion .
| Die ursprüngliche Funktionsgleichung | |
| Die 1. Ableitung der Funktion | |
| Bestimmung der Nullstelle der 1. Ableitung durch Gleichsetzen mit null | |
| einsetzen in | |
| berechnen |
Der Scheitelpunkt hat also die Koordinaten .
Scheitelpunktberechnung mittels bekannter Nullstellen[Bearbeiten | Quelltext bearbeiten]
Sind die Nullstellen der quadratischen Funktion bekannt, dann lassen sich die Koordinaten des Scheitelpunktes wie folgt berechnen:
- .
Schnittpunkt mit der y-Achse[Bearbeiten | Quelltext bearbeiten]
Wegen hat der Schnittpunkt des Graphen mit der -Achse die Koordinaten .
Nullstellen einer quadratischen Funktion[Bearbeiten | Quelltext bearbeiten]
Die Nullstellen einer quadratischen Funktion ergeben sich durch Lösung der Gleichung , das heißt der quadratischen Gleichung
- .
Diese lassen sich mit Hilfe der abc-Formel berechnen:
Nimmt der Ausdruck unter der Wurzel (Diskriminante) einen negativen Wert an, so bedeutet dies, dass keine (reellen) Nullstellen existieren.
Umkehrfunktion[Bearbeiten | Quelltext bearbeiten]
Weil die Parabel nur für die Bereiche und monoton ist, ergibt sich für jeden Bereich (jeden Ast der Parabel) eine Umkehrfunktion, welche zusammen ausgedrückt werden kann mit
- =
mit reellen Werten für
- bei oder bei
Nullstellen und Linearfaktoren[Bearbeiten | Quelltext bearbeiten]
Sind und die Nullstellen der quadratischen Funktion , so kann man die Funktionsgleichung auch als Produkt ihrer Linearfaktoren schreiben:
Schnittpunkt von Parabel und Gerade[Bearbeiten | Quelltext bearbeiten]
sei die Funktionsgleichung einer Parabel und die einer Geraden. Ansatz: gleichsetzen der Funktionsgleichungen quadratische Gleichung. Falls nun:
- Die Parabel und die Gerade schneiden sich in zwei Punkten (Sekante).
- Die Parabel und die Gerade berühren sich in einem Punkt (Tangente).
- Die Parabel und die Gerade haben keinen Schnittpunkt (Passante).
Schnittpunkt zweier Parabeln[Bearbeiten | Quelltext bearbeiten]
seien die Funktionsgleichungen zweier Parabeln. Ansatz: gleichsetzen der Funktionsgleichungen quadratische Gleichung. Falls nun:
- Die Parabeln schneiden sich in zwei Punkten.
- Die Parabeln berühren sich in einem Punkt.
- Die Parabeln haben keinen Schnittpunkt.
- ist eine lineare Gleichung Die Parabeln haben einen Schnittpunkt.
Quadratisches Polynom[Bearbeiten | Quelltext bearbeiten]
Sei ein beliebiger Ring. Als quadratische Polynome über bezeichnet man Ausdrücke der Form
mit und . Formal handelt es sich um Elemente des Polynomringes vom Grad 2, sie definieren Abbildungen von nach . Im Fall handelt es sich im obigen Sinne um quadratische Funktionen.
Falls ein algebraisch abgeschlossener Körper ist, zerfällt jedes quadratische Polynom als Produkt zweier Linearfaktoren.
Allgemeiner sind quadratische Polynome in Variablen Ausdrücke der Form
- ,
wobei nicht alle Null sein sollen. Diese Polynome definieren Abbildungen von nach . Ihre Nullstellenmengen im werden als Quadriken bezeichnet, im Fall auch als Kegelschnitte.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Karin Hantschel, Lutz Schreiner, Michael Bornemann, Wiebke Salzmann: Wissen – Üben – Testen: Mathematik 9. Klasse. Bibliographisches Institut, 2017, ISBN 9783411912315, S. 27–34
- Heinz Rapp: Mathematik für die Fachschule Technik. Springer, 2015, ISBN 9783834809148, S. 156–170












































































![{\displaystyle ax^{2}+bx+c\in R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/045b6862a605c90b9c28693870bd31d3be9aecb8)




![{\displaystyle \sum _{i,j=1}^{n}a_{i,j}x_{i}x_{j}+\sum _{i=1}^{n}b_{i}x_{i}+c\in R[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b5d7568dc19b11f98a510d7b60c9f89407eb9e9)


